Lecture 6: Deterministic Finite-State Automata, Shopping Cart Example

During the past two lectures, we've been talking about keeping state information around, be it in files, memory, database server, or some weird exchange between the browser and server. Today, I'm going to tell you how to construct simple abstract notions of state - this might help you a lot in figuring out what you need to do in the project (and the stuff I'm asking you to write).

First, let's formally define state. State is the way the world looks at any given time. Because the world is kind of big, we normally want to look at subsets of the world. So let's start simple.

Let's say that our world consists of a box and two balls (a red one and a blue one). You can put one or both balls inside the box at any time, and that's all you can do. So now, ask, what are all possible states of this world?

  1. Both balls outside the box. [ROBO]
  2. Red ball inside box, blue ball outside box. [RIBO]
  3. Blue ball inside box, red ball outside box. [ROBI]
  4. Both balls inside the box. [RIBI]

Each one of these is a particular state. Computer science theorists draw graphs of states, with each state being a node (a circle). So let's do that, labeling our states ROBO, RIBO, ROBI, and RIBI (Red In/Out, Blue In/Out).

Okay, so now we want to model how the world changes. Remember that one of these is how to the world looks at any given time. Let's say that we're allowed to move a single ball inside or outside the box. So if we started with ROBO, we could move the red ball into the box. When you do that, you move from state ROBO to state RIBO. That is called a transition.

We denote a transition on our graph as an arrow from ROBO to RIBO, and label the arrow with something like "moved red":

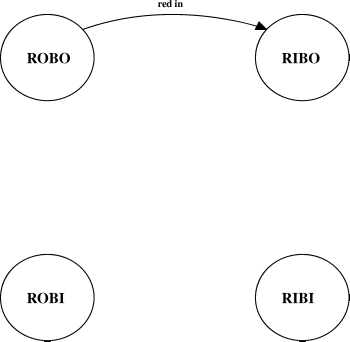
Of course, we could move any ball inside, so we need to draw a couple more transitions.

[more drawing]
Also, we can move the balls outside the box, so that makes four new transitions..

[more drawing]
You need a start state. You just denote that with a "Start" arrow (not shown here):

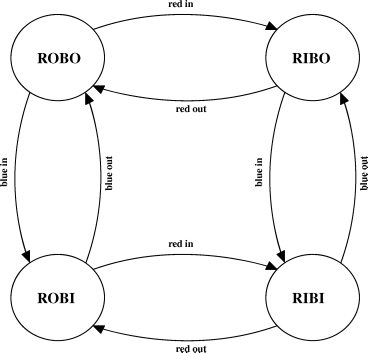
(Interesting aside: if we could pick up two balls with the same hand at once, we'd have two more transitions. But I digress.)

Believe it or not, we've just modeled a computing system with two bits of memory and two instructions (an instruction for flipping each bit). But let's ignore that for now and try to relate this back to web programming.

Because we have these nice pictures on the web, we can visualize the states in this little example with web pages. We can use use a bunch of tables: 

<table>
 <tr>
  <td width=300 height=200>
      <img src=red.gif>
      <img src=blue.gif>
  </td>
  <td width=300 height=200>
    <table border=5 width=300 height=200><tr><td>
    </td></tr></table>
  </td>
 </tr>
</table>
And you could just make four files, robo.html, ribo.html, robi.html, and ribi.html. You can also do the state transitions by using anchor tags around the <img> tags: 
    <a href=ribo.html><img src=red.gif border=0></a>
    <a href=robi.html><img src=blue.gif border=0></a>
So if we click on the red, we move it into the box, click on the blue, we move that inside the box -- just by going to another web page.

Now this doesn't look so bad, you might think, but keep in mind that this is a quite simple task. Making a web page for every single state would just get to be a drag. If, say, we added a black ball to this, we'd get four more states! We don't want to figure out the state transitions between all of those. Thankfully, there is a better way.

We just pass the state information as parameter, as we did before. Let's use PHP. We'll use the parameters "red" and "blue" in GET-method type query strings, and set the values to "in" and "out". (If the parameters are not set, that means we need to set them all to "out" because that's our start position.) 

<table>
 <tr>
  <td width=300 height=200>
     <?php
       if ((!$red) || (!$blue)) {
	  $red="out"; $blue="out";
       }
       if ($red=="out") {
	  print "<a href=\"balls.php?red=in&blue=$blue\"><img src=red.gif border=0></a>";
       }
       if ($blue=="out") {
	  print "<a href=\"balls.php?red=$red&blue=in\"><img src=blue.gif border=0></a>";
       }
     ?>
  </td>
  <td width=300 height=200>
    <table border=5 width=300 height=200><tr><td>
     <?php
       if ($red=="in") {
	  print "<a href=\"balls.php?red=out&blue=$blue\"><img src=red.gif border=0></a>";
       }
       if ($blue=="in") {
	  print "<a href=\"balls.php?red=$red&blue=out\"><img src=blue.gif border=0></a>";
       }
     ?>
    </td></tr></table>
  </td>
 </tr>
</table>
Notice how each one of these if statements is active in exactly two states: for example, the first holds for ROBO and ROBI.

And now we can see that this is really easy to modify if we add a black ball:

[do that]

And notice now that we didn't have to draw the state diagrams. Who cares, we know what the simpler one looks like..

Well, this is a really easy way to imagine this example, but it's possible to get really carried away. Say, for an online store, do we want to visualize every single possible combination of states -- every single combination and quantity of items that we could carry in our shopping cart, and every page we could visit while carrying this shopping cart?

I sure hope not. You should instead think of ways to abstract that down. The example I gave last week with the favorite band is a pretty good illustration. In reality, there are a lot of states and transitions -- in fact, at least three states for each favorite band and a whole lot of transitions. This is all due to the fact that the favorite band could be set to a number of things. But it could be a lot simpler if we realize this: who cares what the favorite band is? We only care if we've picked one or not.

So we have four states, each of which represents a different fundamental appearance on the screen.

  1. No favorite band stored in a cookie, and no band selected.
  2. Favorite band stored in a cookie, but no band selected.
  3. No favorite band stored in a cookie, and new band selected.
  4. Favorite band stored in a cookie, and new band selected.

You can pick these out from the source code with that chain of "if" statements. Take a look.

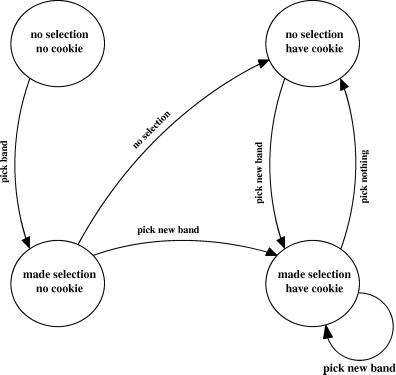
In our guess-a-number game, there are about a zillion actual states because of all of the possibilities for previous guesses, but we can smash it down to five simple states:

  1. Initial board.
  2. Initial guess; no previous guesses.
  3. Wrong guess. Guess is colder than previous.
  4. Wrong guess. Guess is warmer than previous.
  5. Correct guess.

[Figure out the state diagram yourself.]

Now, I'd like to finish our discussion of deterministic finite-state automata, just for the sake of completeness since very few of you have ever seen these things before.

In formal theory, these things operate on strings. Strings are made up by stringing a bunch of symbols from an alphabet together. You start at the start state, and on each transition, you "eat" the next symbol in the string. Each transition corresponds to one or more symbols.

For example, let's operate on an alphabet of "a" and "b" and have three states:

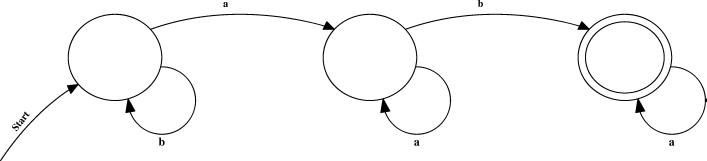
Notice how there aren't state transitions off state 3 for "b". If we get a "b" in state 3, our state machine rejects the string.

So if we're rejecting strings, what does it mean to accept a string? Does it just mean that if we run out of input while we're in the state machine, then we accept it? No. We have to introduce the concept of an accepting state. If we run out of input in an accepting state, then and only then does the machine accept our input.

We denote an accepting state by putting another circle in it.

Now we can see something interesting from this diagram. To accept a string, the machine has to go through these, in this order:

  1. Zero or more "b"s. (at state 1)
  2. One or more "a"s. (to go from state 1 to 2, and to stay at 2)
  3. One "b". (to go from state 2 to 3)
  4. Zero or more "a"s. (to stay at 3)
So we can have ab, aba, abaa, bbaaaabaaaa, and so on and so forth. The set of all strings which the machine takes is called the language of the machine. So there are a whole lot of languages, each of which depends on the machine you use to define it.

We can generalize this even more. These deterministic finite-state automata define a certain class of languages called regular languages. And as it turns out, this is where regular expressions get their name - they represent the languages that these finite-state machines accept. For example, the expression for the above machine is

b*a+ba*

You could put ^ at the beginning and $ at the end if you want to relate it directly to something you'd see in Perl. Neat, huh?

So never say that theory is useless.

Shopping Cart Example

Now let's use what we've learned so far to make a really simple online store. We'll assume that we have a welcome screen (with maybe some specials), a browsable list of items that we can examine more closely and/or put in our shopping cart, the shopping cart itself. If there's something in the shopping cart, we can go to a checkout screen.

First make welcome.php and put the common stuff into util.php.

Then browse.php.

Then view.php.

Then cart.php.