Assignment 1 (due 4/2/2003)

Problem 3(d)

Prove or disprove the following: if d|(a b), then either d|a or d|b.

Problem 5

Write down the converse of the following statement about integers:

If x and y are odd, then x-y is even.

Is the statement you wrote down true or false? Prove your answer.

Problem 8(b)

Prove that x y is odd if and only if x is odd and y is odd.

Assignment 2 (due 4/4/2003)

Problem 2

Describe each of the following sets in terms of a property of its elements:
    (b) {1, 3, 5, 7, 9, 11, 13, 15}
    (d) {1, 4, 9, 16, 25, 36, 49, 64}

Problem 6

Write down the power set for each of the following sets:
    (a) { x, y, z, w }
    (d) { ∅ }

Problem 12

For each of the following expressions, use a Venn diagram representing a universe U and two subsets A and B:
    (a) A'.
    (b) B'.
    (c) (A∪B)'
    (d) A'∩B'
    (e) A'∪B'
    (f) (A∩B)'
Note: The notation A' means the complement of A with respect to U.

Problem 15

Given three sets A, B, and C. Suppose the the union of the three sets has cardnality 280. Suppose also that |A| = 100, |B| = 200, and |C| = 150. And suppose we also know |A∩B| = 50, |A∩C| = 80, and |B∩C| = 90. Find the cardinality of the intersection of the three sets.

Problem 25

Prove that A∪(B∩C) = (A∪B)∩(A∪C).

Assignment 3 (due 4/7/2003)

Problem 11

Try to describe each of the following languages in some way.
    (a) {a, b}^* ∩ {b, c}^*
    (b) {a, b}^* - {b}^*

Problem 16

Prove each of the following statements about combining set operations with Cartesian product.
    (b) (A-B)×C = (A×C)-(B×C)

Assignment 4 (due 4/9/2003)

Problem 4(b)

Draw a picture of the directed graph that corresponds to the following binary relation:

{(a, b), (b, b), (b, c), (c, a)}

Problem 6

Given the following graph

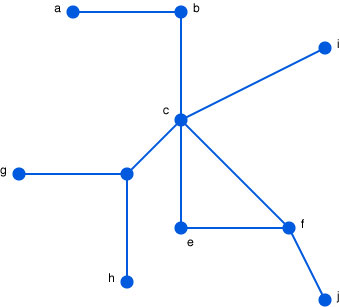
    (a) Write down one breadth-first traversal that starts at vertex f.
    (b) Write down one depth-first traversal that starts at vertex f.

Problem 8

Given the algebraic expression

a × (b + c) - (d / e)

Draw a picture of the tree representation of this expression. Then convert the tree into a list representation of the expression.