


Next: About this document ...
CS 319--The Lambda Calculus
Assignment 1, Winter 2000
Due Monday, 24 January
- Show that application is not associative, i.e., there
exist
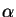 ,
, 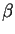 ,
,  such that
such that
To make the
problem slightly more interesting, do it with closed terms.
- Show that there is no selector function
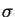 such that, for
all
such that, for
all 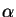 ,
, 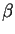 ,
,
- Let each symbol be 0.5 cm wide. Construct a lambda term less
than 20 cm long, whose normal form is at least
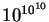 light
years long. The speed of light is
light
years long. The speed of light is
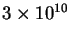 cm/sec. Make
the ratio between the length of the normal form of your term, and
the length of the term itself, as big as you can. Count
cm/sec. Make
the ratio between the length of the normal form of your term, and
the length of the term itself, as big as you can. Count 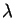 ,
variables, and parentheses, but not the period that we sometimes use
to separate a lambda-bound variable from the body of the lambda
term.
,
variables, and parentheses, but not the period that we sometimes use
to separate a lambda-bound variable from the body of the lambda
term.
- Prove that, if beta-conversion is interpreted with naive
substitution, then
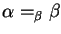 for all
for all 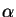 ,
, 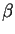 .
.
Mike O'Donnell
2000-01-17