


Next: About this document ...
CS 319--The Lambda Calculus
Assignment 2 Winter 2000
Due Monday, 31 January
- Show how the Turing fixpoint term
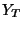 can be used for
mutually recursive functions. That is, given
can be used for
mutually recursive functions. That is, given
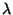 terms
terms
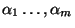 , where each
, where each 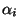 involves the
variables
involves the
variables
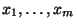 and
and
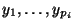 , construct
terms
, construct
terms
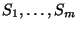 such that
such that
- Generalize the method above to allow definitions analogous to
which defines
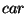 ,
,
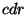 , and
, and
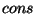 by
a more general sort of mutual recursion.
by
a more general sort of mutual recursion.
- Generalize the solution methods above as much as you can. For
example, certain infinite systems are solvable.
- Define
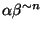 by
by
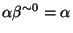 ,
,
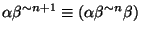 . Define an
alternate encoding of the integers by
. Define an
alternate encoding of the integers by
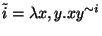 . Prove that
the
. Prove that
the 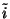 encoding is equivalent
to Church's
encoding is equivalent
to Church's 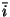 encoding by exhibiting two
translating terms,
encoding by exhibiting two
translating terms, 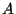 and
and 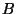 , such that for all
, such that for all 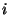 ,
,
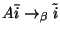 and
and
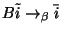 .
.
Mike O'Donnell
2000-01-24