


Next: About this document ...
CS 319 - The Lambda Calculus
Assignment 3, Winter 2000
Due Monday, 7 February
- Demonstrate an interesting encoding of integers in the lambda
calculus that is not suitable for computation.
- Using weak bracket-abstraction, show that the
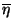 rule below does not imply extensionality.
rule below does not imply extensionality.
- Using weak bracket-abstraction, bound the length of
![$ [x].\alpha$](img5.gif) and of
and of
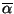 in terms of the length of
in terms of the length of  . Give
examples showing that your bounds are tight. What difference does
strong bracket-abstraction make?
. Give
examples showing that your bounds are tight. What difference does
strong bracket-abstraction make?
- Find out what happens to
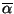 under weak
reduction when
under weak
reduction when  produces nested residuals under beta reduction.
produces nested residuals under beta reduction.
- Continue to work on general classes of solvable equations. You
may do this as a joint project, and hand in a single joint
presentation, if you like.
Mike O'Donnell
2000-01-31