Lab 5: Huffman Coding

CS151 Home

Introduction

Digital information is stored as binary digits -- bits -- and bits are physically represented as high and low electrical signals. Bits are written as 1 and 0, corresponding to high and low respectively. A byte is a bitstring of length 8. The standard ASCII character encoding assigns one byte to each of 256 characters (256 being the number of distinct bytes that can be represented with 0 and 1).

In ASCII, the capital A character corresponds to 01000001 (this is also the binary encoding of the number 65), B to 66, and so on till Z to 90. The following table shows some examples.

character	binary encoding
A	01000001
B	01000010
C	01000011
...	...
Z	01011010

We can represent the characters SHE with eight-bit ASCII codes as follows:

01110011 01101000 01100101

In this lab we will learn an alternative efficient encoding technique that generates shorter message encodings than ASCII. The technique is known as Huffman coding.

Here are some insights relevant to how Huffman coding works. If a message contains only a subset of the set of ASCII characters, it is very likely possible to use fewer than eight bits per character. For example, if our message is simply PIZZA, only four letters are used. Strictly speaking, for PIZZA we only need two bits per character: for example, 00 for P, 01 for I, 10 for Z and 11 for A. Under that scheme, we could represent PIZZA in just ten bits: 0001101011; in plain ASCII, by contrast, we need 8 bits for each of the 5 characters, or 40 = 5 * 8 bits.

A second insight: if possible, we would like our more frequent characters to have shorter encodings than less frequent characters. Huffman codes use variable-length encoding for characters; not all characters are represented by the same number of bits. At scale, this can result in great savings.

These observations are the main ingredients in the Huffman coding system.

Note that variable-length encodings need to be prefix-free -- that is, the encoding of any character must not be the prefix of the encoding of any another character. This property must hold to ensure than encoded messages can be unambiguously decoded. The Huffman coding scheme produces prefix-free character encodings as a matter of course, so you need only implement the algorithm presented here to maintain prefix freedom.

To determine the Huffman codes for our characters, we start by counting the number of occurrences of each letter in the message. Consider the message SHESELLSSEASHELLS. The corresponding frequencies would be (A 1), (H 2), (E 4), (L 4), (S 6). With this list of frequencies we construct a Huffman tree by following this procedure:

1. Construct a sorted (ascending, by weight) list of singleton Huffman trees, with weights given by the calculated frequencies.
2. Extract the two trees with the smallest weights from this list.
3. Merge the two extracted trees into a new tree, whose weight is the combined weight of the two subtrees.
4. Insert the newly-created tree back into the list such that the list still remains sorted by weight.
5. Repeat from step 2, until only 1 tree remains in the list.

When only one tree remains in the list, we are done. That tree will be the mechanism by which we both encode and decode messages.

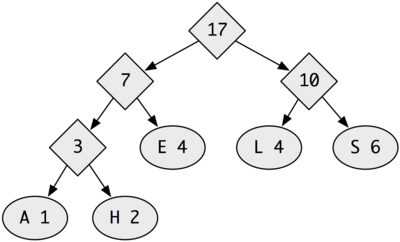
Running this algorithm on our example (SHESELLSSEASHELLS) produces the following tree:

To encode a string, we compute the bitstring for each character by traversing the path from the root to that character. Every time we move to a left subtree we record a 0, and every time we move to a right subtree we record a 1. For example, for this tree, we derive 001 for H.

To decode an encoded bitstring, we must be given both a bitstring and a Huffman tree. We start at the root, and move down and left for each 0, and down and right for each 1. Every time we reach a leaf, we record the letter at that leaf, and return to the root to begin reading the next letter.

Try to read the word 01011011 from the tree above. (It's something slimy.) What about 00101011011?

To facilitate implementation, we will build augmented Huffman trees such that each leaf contains the bitstring representing the path to that leaf. This will ease the encoding process in particular. The "augmented Huffman tree" corresponding to the tree above is this:

Note that the more frequently occurring letters have shorter bit encodings.

To check your understanding of Huffman coding, verify the following results with pen and paper:

• FOO --> 011
• HUBBUB --> 000111011
• REFEREE --> 0110010111

For today's exercise, assume that messages consist only of uppercase letters and spaces.

Part 1: Construct the Tree

Download the lab 5 starter file for some basic data definitions.

Write code to implement the following steps:

• Given a message, generate a list of character/number pairs, where each number is the occurrence count of that character.
• Given a list of character/number pairs, produce the list of corresponding "singleton trees". Each such tree should have the empty list as its path.
• Sort the list of singleton trees in ascending order by count.
• Coalesce the list of trees into one big tree according to the algorithm sketched above (right above the first tree figure). Every time your program merges two trees, it must update the paths at the leaves accordingly.

Part 2: Decoding

Write a function

decode : list-of-bits huff -> string

to decode a given encoded message.

Part 3: Encoding

Write a function

encode : string -> (pair-of list-of-bits huff)

to encode a plaintext message and return both the bitstring and the Huffman tree corresponding to that encoding.

When all is said and done, you should be able to feed strings into the following function and get those same strings back.

;; round-trip : string -> string
;; encode and then decode a message
(define (round-trip msg)
  (local {(define p (encode msg))}
    (decode (pair-of-item1 p) (pair-of-item2 p))))


Submitting: Note Extended Deadline

Submit your work via CS151 Handin by 10 PM on Tuesday, Nov 16. Make sure your work is submitted as Lab5. Good luck, everyone.