This assignment should be done using the Advanced student language.
In this project you will implement an animated version of the A* search algorithm. A* is a classic Artificial Intellegence algorithm that is often used for puzzle solving and for pathfinding in computer games. You will use A* to find a path through a maze.
This project will require significant use of imperative data structures in your implementation.
Make sure that your submitted solution compiles; i.e., that there are no syntax errors or undefined variables. Submissions that do not compile will get 0 points!!!
The A* algorithm is a directed search algorithm that uses a best-first strategy to find the lowest cost path from a start node to a goal node. The algorithm works by partitioning the graph nodes into three sets:
Initially, the set of closed nodes is empty, the set of open nodes consists of the start node, and all other nodes are unknown.
The open nodes are kept in a priority queue, which is ordered by the cost function f(nd) = g(nd) + h(nd), where
For this project, the cost of moving from a node to its neighbor is one, thus g(nd) measures the length of the path from the start node to nd.
A single step of the A* algorithm proceeds as follows:
Your program will consist of four parts: the concrete representation of the part of the graph that the algorithm has explored, the world data structure that holds the state of the search, the code to implement a single step of the A* search, and the user interface. We describe each of these parts below.
Your implementation of A* will be searching over an abstract graph that is defined by a maze data structure (see below). Each node in the graph corresponds to a tile in the maze. You will need to define additional data structures to represent the part of the graph that has been explored.
A tile-node's status is one of 'open, 'closed.
A tile-node consists of the tile's location (location), status (tile-node-status), cost or g() value (num), and previous node (one of #f or tile-node). Note that by traversing the previous node links from the goal node, we can determine the path that was discovered by the search.
The open set is represented by a priority queue of tile-nodes (see below). As described above, the priority function is the sum of the cost of the path from the start to the node, which is stored in the node, and a heuristic estimate of the cost of the path from the node to the goal. For A* to return the shortest path, it is necessary for the heuristic to be admissible, which means that it cannot over estimate the cost. We will use the Manhattan distance to the goal as our heuristic. This heuristic is both admissible and monotonic (or consistent); this latter property allows us to use a simpler version of the A* algorithm that does not reopen closed nodes.
We will not keep a representation of the closed nodes; rather, we will keep track of all of the nodes that have been visited (i.e., the union of the open and closed sets). For this purpose, we will use a hash table that maps the location of a tile to the graph node that represents it.
A world consists of five fields:
where the world mode is one of 'stepping, 'running, 'success, or 'stuck.
You should define two helper functions on worlds. The first is used to detect when the simulation has finished; either because it is successful or because it failed.
;; world-done? : world -> boolean ;; return true if the search is finished; i.e., the mode is 'success or 'stuck. (define (world-done? wrld) ...)
The second function is used to create and initialize a new world object for a maze. This function is also responsible for initializing the A* search (i.e., creating an initial tile-node for the start location and including it in the open set and hash table.
;; new-world : maze -> world ;; create and initialize new world for the given maze. (define (new-world maze) ...)
Your implementation of A* should be designed to advance the search by one step as described above. This function has the following header:
;; A*-step : world -> world ;; Take one step of the A* algorithm. Note that we assume that the world ;; is either in 'stepping or 'running mode. (define (A*-step wrld) ...)
Note that although it returns a world, it should always return the world object that it is given and use imperative update to change the state of the world.
An important part of the A* step is the processing of neighbor nodes, which you may want to split into its own top-level function.
;; process-neghbor : world tile-node -> location -> void ;; check neighboring locations to the tile-node nd. This includes checking ;; to see if there is already a tile-node for the location and, if not, creating ;; one and adding it to the open set. (define (process-neighbor wrld nd) ...)
Because these functions are imperative, you are not expected to define check-expects for them.
One tricky issue is what to do if when processing a neighbor node, you discover a shorter path to an already open node. The way to handle this situation is to first update the cost and previous-node fields of the neighbor and then to reinsert it into the priority queue. This will result in duplicate entries in the priority queue, but you handle this issue by checking in A*-step to see if the node you remove from the open set is already closed. In that case, it is a duplicate and you should ignore it and get another node (i.e., recursively call A*-step again).
Your program should support two modes of performing the search. Initially, your program should be in 'stepping mode, where the search is advanced one step each time the user types the space key. If the user types the "r" key, then the mode should be switched to 'running, where the search steps automatically until it either finished. If the mode is 'running and the user types the "s" key, then the mode should be switched back to 'stepping.
We will use the big-bang function from the universe teachpack to drive the animation. You should package it up in a run function as follows:
;; run : string -> void ;; Run the A* animation on the maze defined by the named file. (define (run filename) (begin (big-bang (new-world (load-maze filename)) (on-tick step-on-tick 1/5) (on-key step-on-key) (to-draw render-world) (stop-when world-done?)) (void)))
The step-on-tick and step-on-key functions are used to control the stepping of the search depending on the current mode. The step-on-key function also must handle mode changes.
Your code will be responsible for rendering the state of the world at each step. This task is handled by the render-world function, which has the following header:
;; render-world : world -> image ;; render the world as an image. (define (render-world wrld) ...)
You rendering code should mark the open and closed nodes and should report on the current state of the search (i.e., how many steps have been taken, etc.). When the search has completed successfully, it should render the resulting path.
We have provided a number of definitions to help with the rendering (see below). You will also want to write a function for rendering the path from the goal node back to the start node.
;; render-path : image tile-node -> image ;; render the path from the node nd (presumably the goal) to the start node (define (render-path img nd) ...)
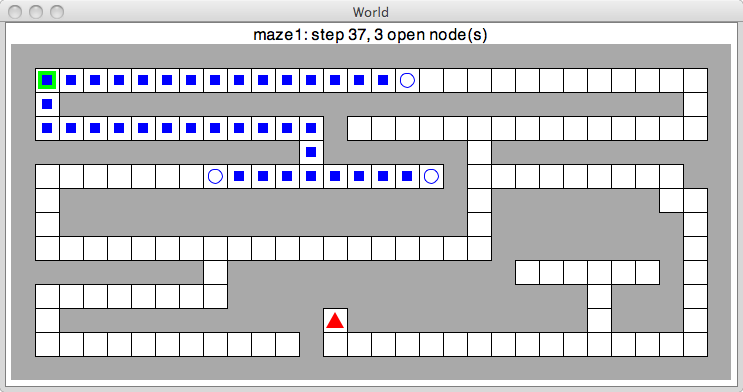
Here is an example of what the application looks like while the search is in progress.

The green square marks the start node and the red triangle marks the goal. Open nodes are marked by circles and blue squares signify closed nodes.
Here is an example of what it looks like after the search is complete.
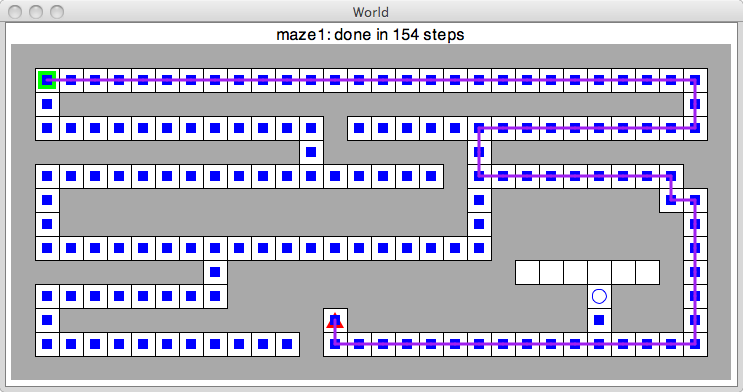
The path from the goal back to the source is drawn in purple.
This file contains utility code and data structures that you will need for your solution. The details of this code are described below.
We provide several test maze files for you to run your program on. You should place these files in the same directory as your project source file; you can then test your code on a maze by the expression
(run filename)
Here is a list of the test mazes, along with the number of steps that my code takes to find the solution and the length of the shortest path. Note that your number of steps might be off by one or two, but that your code should find a path of the same length.
| Maze | Number of steps | Path length | Description |
|---|---|---|---|
| maze0 | 33 | 33 | a completely open maze with no interior walls |
| maze1 | 154 | 73 | the maze pictured above |
| maze2 | 150 | 53 | a partially open maze with only a few walls |
| maze3 | 49 | 18 | a partially open maze with only a few walls |
| maze4 | 82 | 37 | is a variation on maze3 |
| maze5 | 74 | 36 | is a subtle, but significant variation on maze4 |
You will find the various types and operations described below useful in your implementation.
;; a (priority-queue X) is an collection of X values ;; that are ordered by priority (define-struct priority-queue (...)) ;; pq-new : (X -> num) -> (priority-queue X) ;; Create a new empty priority queue that uses priority-fn to order ;; the elements of the queue (define (pq-new priority-fn) ...) ;; pq-count : (priority-queue X) -> nat ;; return a count of the number of items in the priority queue (define (pq-count pq) ...) ;; pq-empty? : (priority-queue X) -> boolean ;; return #t if the priority queue is empty (define (pq-empty? pq) ...) ;; pq-insert : X (priority-queue X) -> void ;; insert an item into a priority queue (define (pq-insert item pq) ...) ;; pq-next : (priority-queue X) -> (oneof X #f) ;; remove and return the item with the lowest priority from the queue (define (pq-next pq) ...)
;; A location in a maze is (define-struct location (row ;; : nat -- the location's row col)) ;; : nat -- the location's column ;; location-add : location location -> location ;; location addition (define (location-add loc1 loc2) ...)
;; a tile is either a 'wall or 'open ;; A maze is (define-struct maze (name ;; : string -- the name of the maze tiles ;; : (matrix tile) -- a matrix of tiles start ;; : location -- the start location goal)) ;; : location -- the goal location
;; neighbors : maze -> location -> (list location) ;; return a list of the non-wall neighbors of a tile (define (neighbors maze) ...)
;; load-maze : string -> maze ;; load a maze from a file (define (load-maze filename) ...)
The project3-starter.rkt file also contains support for rendering mazes.
;; tile icons are images that represent the state of known nodes (define open-icon ...) (define closed-icon ...) ;; render-maze : string maze -> image ;; render a maze and its title as an image (define (render-maze title maze) ...) ;; overlay-tile : image location image -> image ;; overlay image over on image under centered on the tile with the given location. (define (overlay-tile over loc under) ...) ;; render-edge : image location location -> image ;; render a path edge between the two locations over the given image (define (render-edge img loc1 loc2) ...)
Hash tables are part of DrRacket, but we describe the operations on them that you may find useful, since you may find the DrRacket documentation confusing.
;; make-hash : (list (list X Y)) -> (hash X Y) ;; Create a new hash table initialized by a list of key/value pairs, which ;; are represented as two-element lists. (define (make-hash assocs) ...) ;; hash-has-key? : (hash X Y) X -> boolean ;; Returns #t if the hash table has a mapping for the given key value (define (hash-has-key? hash key) ...) ;; hash-ref : (hash X Y) X -> Y ;; returns the value that the hash table maps key to. This function signals ;; an error if there is no mapping for key. (define (hash-ref hash key) ...) ;; hash-set! : (hash X Y) X Y -> void ;; imperatively add a mapping from key to value to the hash table. (define (hash-set! hash key value) ...) ;; hash-map : (hash X Y) (X Y -> Z) -> (list Z) ;; Map a function over the elements of a hash table, returning a list of the results. (define (hash-map hash f) ...)
Last revised: December 5, 2010.