Lab 4 will be collected from your subversion repository on Monday, October 24, at 5pm.
Work in the file lab4/lab4.rkt. It is important that this file has exactly this name and location; we will be looking for your work under this name at collection time.
Today's exercise concerns linear regression. The problem is well-suited to being decomposed into a set of related functions. The lab exercise description does not specify too closely which individual functions you should write; this is to give you practice with program design.
At the beginning of lab your TAs will explain the basic concepts of linear regression, the notation used in this write-up, and how to use a spreadsheet application to generate results against which you can test.
Modeling Datasets
You will need three data definitions in order to do this exercise:
datum, dataset and
datum will consist simply of an x and a y.
(Why not just use posn? Semantics!)
A dataset will consist of a nonempty list of
datums. A
A linear regression analysis is applied to a set of data; its result
is the line that mathematically best fits the data as it would appear
on a two-dimensional plot. Operationally, with linear regression
analysis, you put a dataset in and get a linear equation out. Your
goal is to write a function linreg whose contract is
Linear Regression
In the following discussion, assume that n is the number of datums in the given dataset.
The best-fit slope for the linear model of a dataset is given by
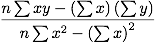
The y-intercept for the linear model of a dataset is given by
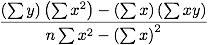
The two formulas above can be expressed as functions, with the following contracts:
Your design will inevitably involve helper functions. The helper
functions you will need to write in order to get linreg
to work will mostly be structurally recursive functions that follow
the How to Design Programs template closely.
When you have finished linreg, you have finished the lab.
Commit as usual.
Hints
- Define a few simple test datasets for your tests. They'll save space and improve clarity.
-
Write
sum : numlist -> num. You'll use it. -
This exercise is full of opportunities to use
map. - The mathematical notation in this lab is terse. If you find the notation confusing or unclear, ask TAs and fellow students (it's well within academic honesty boundaries to ask fellow students for help with notation) for explanation.
Extra Credit: The Linear Correlation Coefficient
A full linear regression analysis includes the computation of a linear correlation coefficient. This coefficient is usually referred to as r and is a measure, roughly speaking, of "how linear the data is." Typically a linear regression analysis provides the value r2, which lies in the interval [0,1]. The closer r2 is to 1, the stronger the correlation between the data and the line modeling the data. An r2 close to 0 means that the analysis has calculated a linear equation that bears no meaningful relationship to the data at hand.
An analysis will be a struct
consisting of two parts: a lineq and
a num, the latter being the
The linear correlation coefficient r is given by the following:
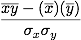
- The standard deviation is the square root of the variance, where
- the variance of a set of numbers is the is the mean of the squares minus the square of the mean.
Note: the formula above gives r; the full analysis returns r2 .
Do not skip ahead to extra credit. We will award extra credit when we see a working version of full-linreg and, furthermore, you have earned full or very nearly full credit on the main part of the exercise (linreg).
Acknowledgements
This programming exercise grew out of similar exercises developed in collaboration with faculty (of whom I was one) at the Dwight-Englewood School in Englewood, NJ.