Genetic Algorithm: UChicago Meals and the Knapsack Problem

Introduction

Genetic algorithms fall under the umbrella of evolutionary algorithms: a group of algorithms that use biologically inspired methods to solve problems. Specifically, genetic algorithms simulate natural selection in order to provide an imperfect solution to a complex optimization problem, generally one that does not have a fast polynomial-time solution. Through an iterative process, a genetic algorithm kills off low quality solutions within a generation (a set of possible solutions) and allows the most fit (highest quality) solutions to survive to the next generation and combine to reproduce new solutions. When working properly, the average fitness of each generation improves over many iterations, and the process continues until an adequately fit solution has been generated.

Genetic algorithms are frequently deployed in a variety of practical contexts. Applications include:

• Engineering: including design of a NASA spacecraft antenna shaped to optimize radiation pattern.
• Bioinformatics: including RNA structure prediction and multiple sequence alignment.
• Financial Mathematics: including technical analysis of stock market trends.
• Scheduling: including assignment of teachers and students to various time slots for classes.

Genetic algorithms are most useful for problems with the following characteristics:

• Solutions can be easily encoded and represented.
• For each solution, a numerical score can be calculated to evaluate quality.
• The set of possible solutions is large, complex, and multi-dimensional, and an optimal solution is not obvious.
• A perfect solution is not required; a good solution is adequate.

The Knapsack Problem

For this programming assignment, you will write an implementation of a genetic algorithm that solves an application of the Knapsack Problem. The Knapsack Problem is a discrete constrained optimization problem that asks the following question: given a set of items, each of which are assigned a weight and value, what combination of items maximizes the value of items placed in the knapsack while remaining below a given total weight? In other words, given a value (\(v_i\)) and weight (\(w_i\)) for each item and total weight (W), pick each \(x_i\) to solve:

Note that your solution (x) is a vector of binary integers. For each item, a corresponding 1 in the solution vector implies that the item is placed in the knapsack, while a corresponding 0 implies that the item is not placed in the knapsack. You may not put multiple copies of the same item in the knapsack.

There are two aspects of this problem:

• A decision problem: can a value of at least V be attained without exceeding the weight limit W?
• An optimization problem: what is the solution that maximizes V without exceeding the weight limit?

For this programming assignment, you will solve the optimization problem. Specifically, you will iteratively perform the genetic algorithm 100 times and pick the individual solution with the highest value that meets the weight restriction.

Terminology

Here is some terminology specific to the genetic algorithm:

• Solution - a combination of items.
• Gene Sequence - a genetic representation of a solution, in this case an array of binary integers.
• Generation - the group of all solutions for a given iteration.
• Gene Pool - the group of gene sequences that genetically represent a generation, in this case an array of pointers to gene sequences.
• Weight Coefficients - an array containing the weight of each item in the knapsack; it provides coefficients for the gene sequence when solving for the total weight of an individual solution.
• Value Coefficients - an array containing the value of each item in the knapsack; it provides coefficients for the gene sequence when solving for the total value of an individual solution.

Digression on Gene Pools

This assignment will involve substantial interaction with gene pools. We will briefly describe the best way to visualize a gene pool to reduce confusion.

A gene pool is a group of gene sequences. Since a gene sequence is a one-dimensional array of binary integers, there are two equivalent ways to conceptualize a gene pool: 1) as a two-dimensional array or 2) as an array of pointers to gene sequences.

The second way of visualizing a gene pool makes more sense for this assignment. Each individual gene sequence represents a solution to the knapsack problem, so a gene pool is just a convenient way to keep track of several solutions. Within this context, the idea of a "column" does not apply to the gene pool -- we care about each individual solution independent of its relationship to the others. Given this interpretation, it will be helpful for you to visualize the gene pool structure in the following manner:

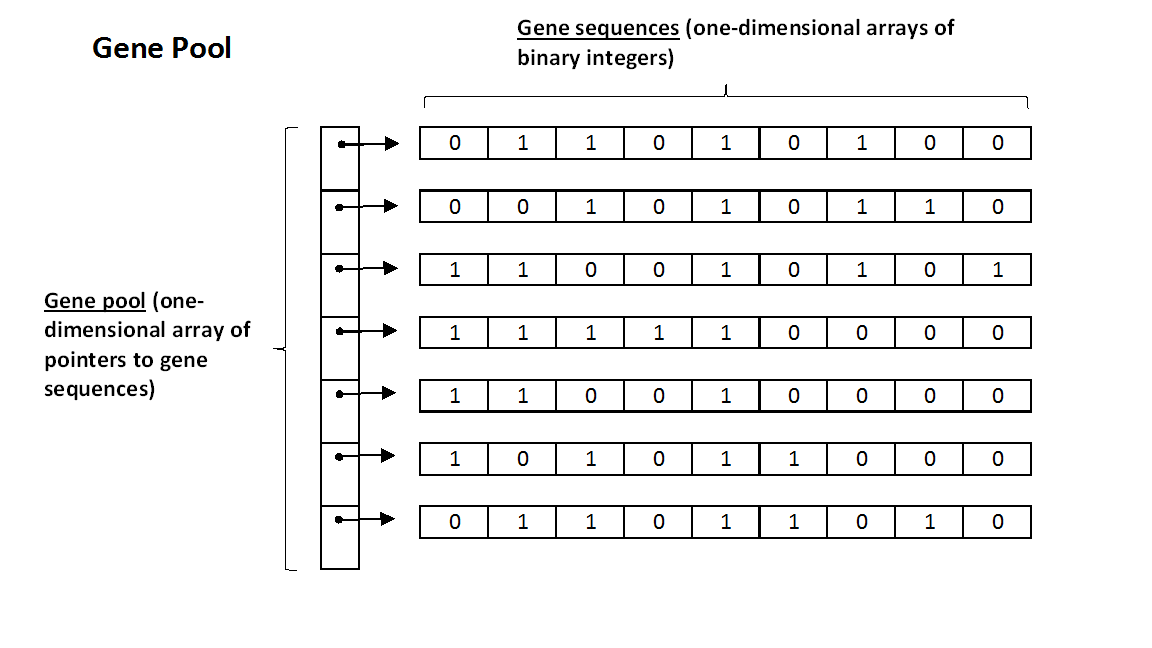
Implementation

We will first explain how to implement a genetic algorithm to solve the Knapsack Problem, and we will then explain how to tweak the implementation to solve the Diet Problem. The Knapsack implementation of the genetic algorithm involves three major steps:

1. A Fitness Function

You will receive an initial randomly-generated population of individuals represented by a gene pool. The first step of the algorithm is to write a function that determines which individual solutions will survive and inserts them into the next generation. This task involves:

1. Computing the total weight and total value for each individual solution. For each individual solution, this computation involves taking the dot product of the corresponding gene sequence with the weight and value coefficient arrays. The dot product of two vectors A = [\(A_1, A_2, ...\: A_n\)] and B = [\(B_1, B_2, ...\: B_n\)] is defined as:

2. Using insertion-sort to place the gene sequences into the new generation in order of highest to lowest value. The insertion-sort should adhere to the following criteria:

   1. If a gene sequence does not satisfy the weight requirement, it should not survive, meaning that it should not be inserted into the next generation.
   2. After having executed the insertion-sort, there should be a maximum of n gene sequences in the new generation, where n is the maximum number of survivors per generation (given). Keep track of the number of survivors after each insertion. Among the gene sequences that satisfy the weight requirement, your insertion-sort should place the top n by value into the next generation.

   Note that there are two main ways to think about insertion-sort in the context of this assignment. In both cases, your insertion-sort function will be given a gene pool and will have to fill in an empty gene pool (an array of NULL pointers) with gene sequences properly ordered by value. In both cases you will need to eventually free the old gene pool without also freeing the gene sequences contained in the new gene pool. Consider two methods of implementing the insertion-sort:

1. Insertion-sort with duplicate gene - This method of implementation takes a single gene sequence, finds its position in the new gene pool, then duplicates the gene sequence (allocates a new array using malloc and copies over the values from the gene sequence) and points the corresponding element of the new gene pool to this duplicate array. With this implementation, you can safely free the original gene sequence once you are done duplicating it without modifying the new gene pool. Below is an example (note that the values are arbitrary and for instructive purposes only):

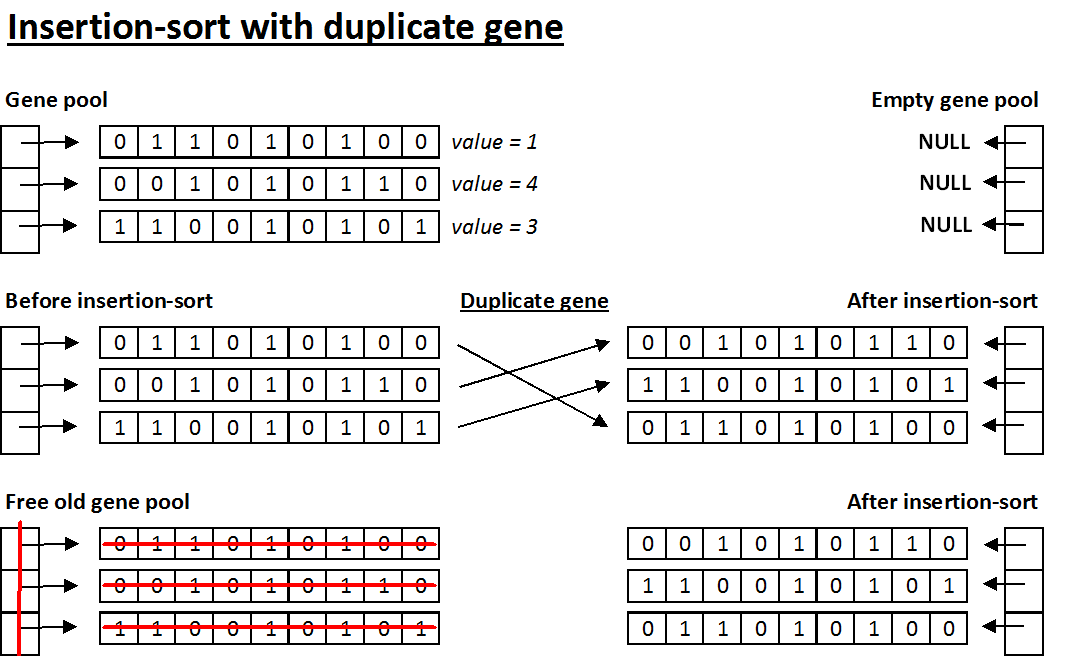
2. Insertion-sort passing pointers - This method of implementation takes a single gene sequence, finds its position in the new gene pool, and points the corresponding element of the new gene pool to the gene sequence. With this implementation, you must set each element of the old gene pool equal to a NULL pointer before freeing the overall structure. That way, when you free the old gene pool, the gene sequences that have been migrated to the new gene pool will not be improperly freed.

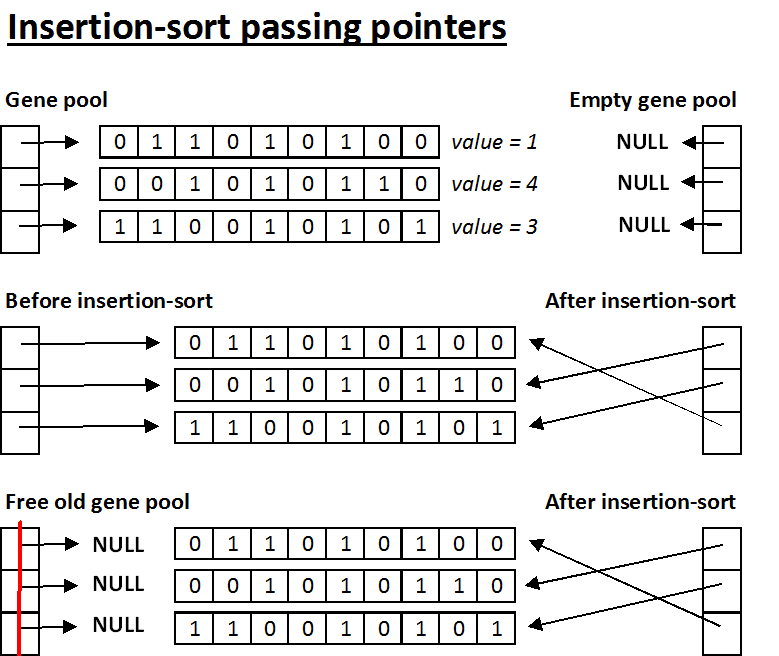
You may use either of these insertion-sort implementations in your code. However, if you are interested in taking CMSC 154, we strongly advise that you implement your insertion-sort by passing pointers.

2. Reproduction

Once the surviving individual solutions have been inserted into the new generation, you will need to populate the empty portion of the population with new individual solutions until all empty spaces for solutions have been filled. You will accomplish this task by randomly selecting two survivors and breeding them to produce children. No parent (survivor) should ever breed with itself. This restriction implies that the two parents should never be drawn from the same position in the gene pool. However, it is possible that two parents drawn from different positions in the gene pool may be identical (ie. the survivors occupying elements 0 and 1 of the gene pool may be identical); in this case, these two parents may breed. If your function randomly draws two parents from the same position in the gene pool (ie. both parents are drawn from element 3 of the gene pool), you must randomly redraw both parents. Breeding involves:

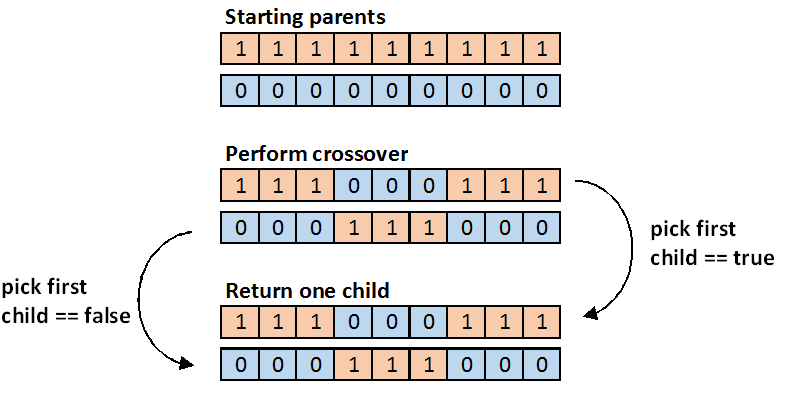
1. Crossover: given two parents, crossover produces two children by switching the middle elements of the two parents. If m is the number of elements in the gene sequence, then we define middle as all of the elements between (not inclusive) low_cross and high_cross, defined as follows:

int low_cross = m / 3 - 1;
int high_cross = 2 * (m / 3);

For example:

2. Mutation: given one child, randomly mutate each element of the gene sequence with probability \(\frac{1}{m}\), where m is the number of elements in the gene sequence. For a specific element of a gene sequence, mutation involves switching a 1 to 0 or a 0 to 1. For example:

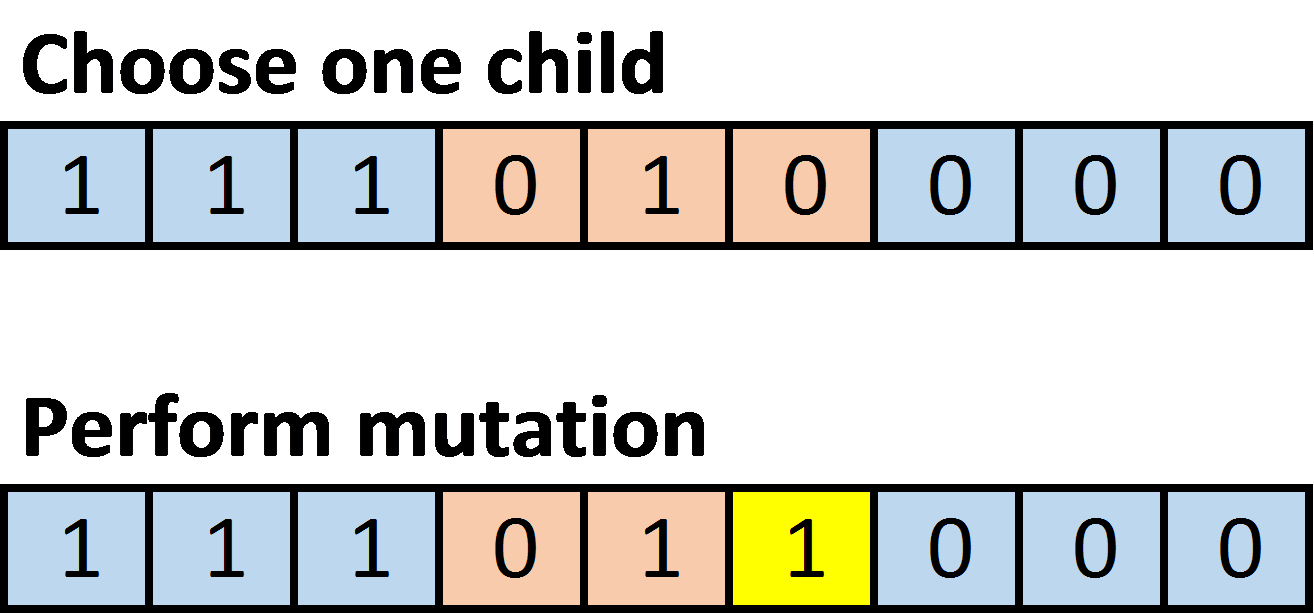
After the crossover, choose one child (with equal probability) for subsequent processing; discard the other. Perform mutation on the chosen child, and then insert it into the new generation.

Note that breeding requires a minimum of two survivors in the new generation after the insertion-sort. If the first new generation does not have at least two survivors (in other words, fewer than two survivors passed the weight requirement), free all data structures currently in use, print an error message, and terminate the program.

3. Iteration

Repeat steps 1) and 2) for 100 generations and return a duplicate of the maximum value gene that meets the weight requirement. Debugging hint: print the average value of each generation (the average value of all gene sequences that meet the weight requirement). If working properly, your average value should increase substantially over the first few generations and fluctuate slightly (to reflect converging solutions altered by mutation) for later generations.

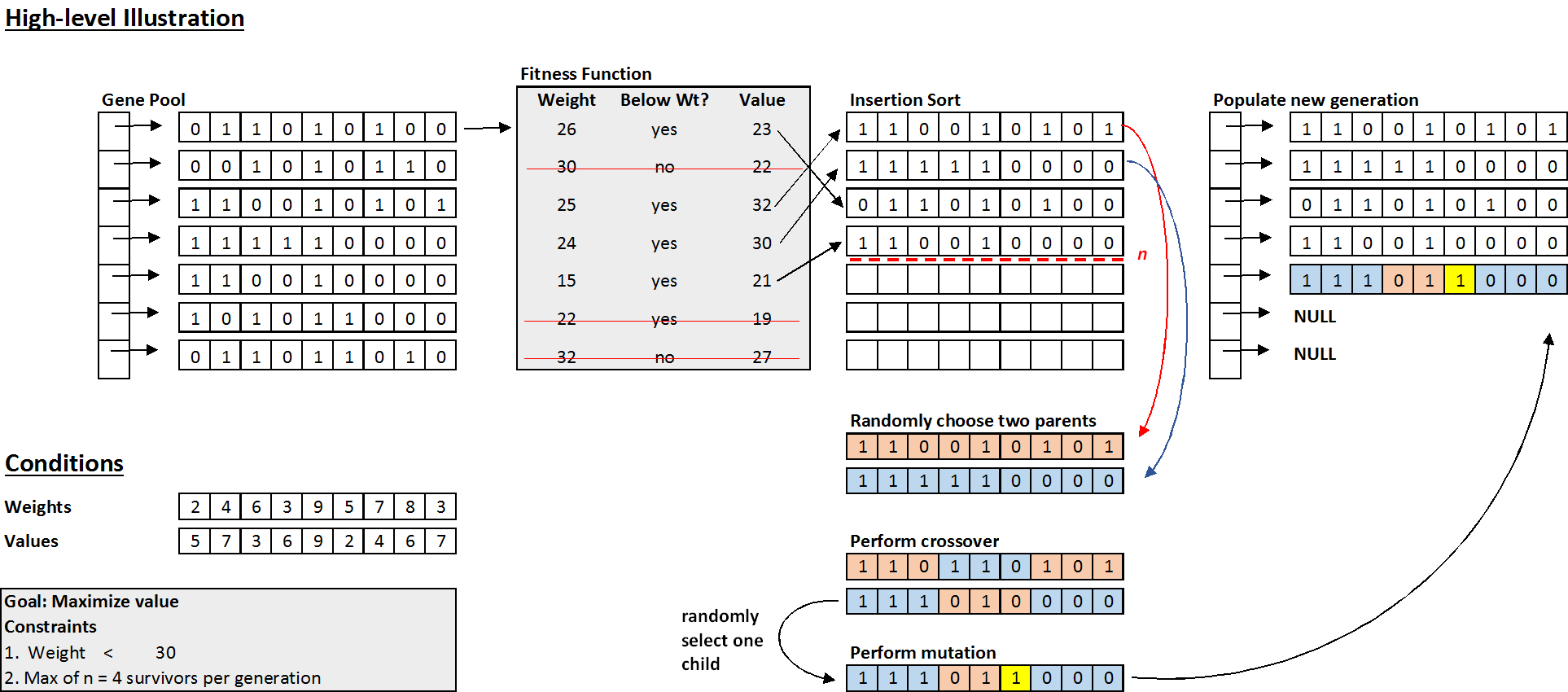
Example of One Iteration

Below is a high-level illustration of steps 1) and 2). In practice, the breeding step would be performed repeatedly until the new generation is fully populated with new individual solutions.

Your Assignment: The Diet Problem with UChicago Dining Data

Your code will use a genetic algorithm to solve an application of the Knapsack Problem: the Diet Problem. The Diet Problem is characterized as follows:

1. You want to assemble a set of food items into a meal and may only consume one portion of each item.
2. You want to maximize your meal's total nutritional value with a preference towards balanced meals.
3. You are constrained by a maximum total number of calories consumed for the meal.

Note that the diet problem can be easily expressed as an application of the knapsack problem. Consider:

In this case, \(v_i\) (previously the value of item i) represents the nutritional value of each item, \(w_i\) (previously the weight of item i) represents the number of calories in each item, and W (previously the weight limit) represents the maximum number of calories allowed for the meal. Solutions (gene sequences) to this maximization problem are also encoded as an array of binary integers: for each item, a corresponding 1 in the solution array means that the item is included in the meal, while a corresponding 0 means the item is excluded from the meal. Given this expression of the diet problem, you can implement the genetic algorithm to solve the diet problem in (almost, see below) the same way you would implement the algorithm to solve the knapsack problem.

We have scraped nutritional data from the UChicago CampusDish website. The raw data appears in the following form:

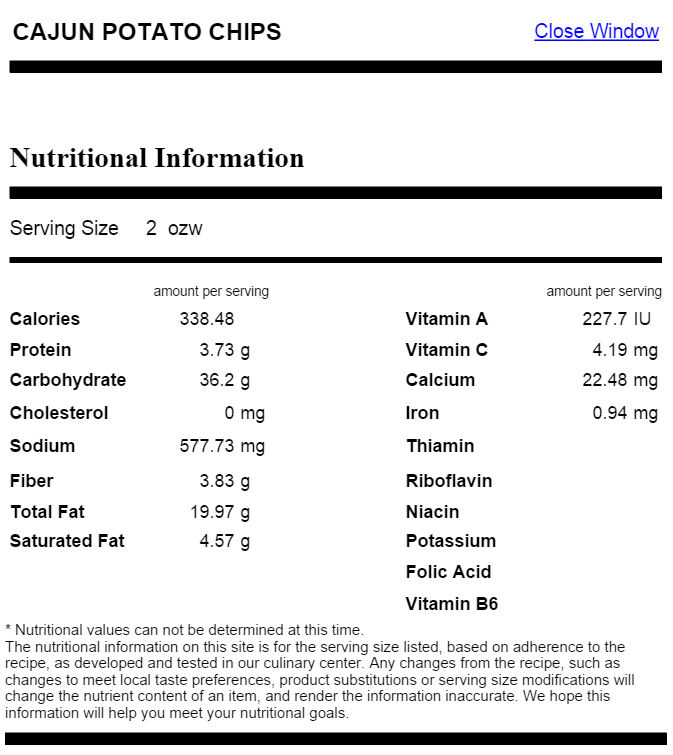
We have converted all of the nutritional information (excluding calories) into percent daily value and saved the data in a file named dining_data.csv. We have provided you with a function mk_wt_val_coef_from_file(char *filename) that takes a filename (pass in dining_data.csv) and returns a data structure that contains all the necessary nutritional data for the assignment. The nutritional data is stored in two forms:

• double *cals_coef - this one-dimensional array contains the calories for each item (ie. the weight coefficients from the knapsack problem).
• double **nutrition - this two-dimensional array contains the non-calorie nutritional information for each food item. Each row corresponds to a food item, and each column corresponds to a percent daily value for each nutrient (this takes the place of the value coefficients from the knapsack problem).

Recall that we want our algorithm to prioritize balanced meals. To accomplish this goal, we define a fitness function that takes a meal (encoded as a gene sequence), takes the sum of the percent daily values for each nutrient, and then adds the square roots of each nutrient sum to arrive at the total nutritional value for a given meal. Note that taking the square root of each nutrient sum results in diminishing marginal value of increasing intake of a single nutrient by one percentage-point (ie. you gain more value from increasing your calcium intake from 1-2% daily value than from 100-101% daily value). This method discourages excessive intake of a single nutrient, since the second derivative of your value function with respect to any single nutrient is negative. Given \(N\) as the total number of nutrients, \(M\) as the number of possible food items to choose from, and a set of vectors \(n_1, n_2, ... , n_N\) where \(n_i\) = [\(n_{i1}, n_{i2}, ... , n_{iM}\)] represents each food item's contribution to percent daily value (\(n_{ij}\)) for a given nutrient (\(n_i\)), the function that computes the total value of a meal can be expressed as follows:

We will provide you with the function that performs this calculation. The function compute_meal_value(wt_val_coef_t wt_val_coef, int *single_gene) takes a wt_val_coef structure and a meal encoded as a single gene sequence and returns the total value of the meal. Note that you will still have to write a function to calculate the total number of calories for a given meal.

Getting Started

Your task is to implement a genetic algorithm that runs 100 generations and then returns a duplicate of the maximum value gene. In other words, you will need to simulate a fitness function, reproduction, and iteration for 100 generations. Our test code will run your function with the following inputs: int n = 20, int m = 37, int num_gens = 100, double max_cal = 1000.0 int, max_surv = 10.

We have seeded your git repository with a directory named pa4, which contains:

• algorithm.c, algorithm.h - the files for your implementation of the genetic algorithm.
• gene_pool.c, gene_pool.h - the files containing the data structures we are providing you for working with gene pools.
• test_genetic_algorithm.c, test_genetic_algorithm.h - the files containing test code for your implementation.
• Makefile - a file that describes how to build and run the application.

The file algorithm.c contains skeleton code for the assignment. The algorithm.c and algorithm.h files are the only files you will modify.

Run git pull upstream master to pick up this directory.

Please add your name to the top of algorithm.c before you start this assignment.

A Random Number Generator

Your genetic algorithm will rely on the generation of random numbers. To assist with debugging and simplify the process of drawing random numbers, we have written wrapper functions for the standard rand function in C.

We have provided two functions that you will use to generate random values. Note that you will need to pass a random_t structure into each of these functions.

• int rand_range(random_t random, int n) - this function takes a random_t structure and an upper bound (int n) and returns a random number between 0 and n-1, inclusive.
• bool rand_bool(random_t random, int prob) - this function takes a random_t structure and a probability (int prob) and returns true with probability \(\frac{1}{prob}\).

Additionally, we have provided several functions for seeding the random functions. The test code will pass a seeded random_t structure into the solve function for you, so you do not have to seed a random_t structure yourself. However, in case you would like to seed your own random_t structure for testing purposes, we have provided a description of the random seed functions.

• random_t seed_rand_time() - this function generates a series of random numbers based on the current time. Each time you run your program, this function will seed the rand function with different values, and therefore the result of your genetic algorithm will differ each time the program is run. The function returns a random_t structure.
• random_t seed_rand_specified(int seed) - this function generates a series of random numbers based on an integer starting value. Each time you run your program, your calls to the random wrapper function will return exactly the same values, and therefore the result of your genetic algorithm will be the same each time the program is run. The function returns a random_t structure.
• random_t seed_rand_file(char *filename, char *filename_bool) - this function reads in a list of random numbers from a file and seeds the random wrapper function with these values. Seeding from a file is particularly useful for testing and debugging purposes. The function returns a random_t structure.
• void free_random(random_t random) - this function frees the random_t structure.

Note that you should only seed the random functions once. Calling the seeding functions multiple times will cause the random functions to work improperly.

Data Structures and Functions

We have provided two data structures to assist your implementation.

• gene_pool_t – the gene_pool_t structure points to a gene_pool (int **genes), the dimensions of the gene_pool (int n, int m), and the number of survivors after executing the insertion-sort (int surv_cnt).
• wt_val_coef_t – the wt_val_coef_t structure points to a one-dimensional array that contains the calorie coefficients (double *cals_coef), a two-dimensional array that contains the nutritional data (double **nutrition), a value for the number of nutrients (int m), and a value for the number of food items (int n).

Additionally, we have provided several functions for working with data structures:

• gene_pool_t mk_gene_pool(random_t random, int n, int m, double max_cal) - given a random structure, the number of rows and columns in a gene_pool, and a calorie constraint, this function creates a gene_pool structure. It randomly populates the gene_pool array with arrays of binary integers, which serve as the initial set of solutions (the initial gene pool) for the genetic algorithm. You will use this function only once.
• gene_pool_t mk_empty_gene_pool(int n, int m) - this function mimics the above function, but initializes all elements of the gene_pool array to NULL. The resulting empty two-dimensional array represents the new generation for each iteration and will be filled in using insertion-sort and breeding. You will use this function once per iteration.
• gene_pool_t mk_gene_pool_from_file(char * filename) - this function initializes a gene_pool structure using values from a file. This function is used in the test code.
• gene_pool_t duplicate_gene_pool(gene_pool_t gene_pool) - this function creates a defensive copy (duplicate) of a gene_pool. In other words, the function allocates space for a gene_pool_t structure and int ** array (int **genes) using malloc, copies over values from the original gene_pool, and returns the duplicate gene_pool.
• wt_val_coef_t mk_wt_val_coef(int n, int m, double *cals_coef, double **nutrition) - given the necessary dimensions and input arrays, this function creates a structure that points to the calorie coefficients and the nutritional data.
• wt_val_coef_t mk_wt_val_coef_from_file(char* filename) - this function creates a wt_val_coef structure using values from a file. This function is used in the test code.
• void free_gene_pool(gene_pool_t gene_pool) - this function frees the gene_pool_t structure.
• void free_wt_val_coef(wt_val_coef_t wt_val_coef) - this function frees the wt_val_coef_t structure.

We have also provided you with three auxiliary functions for use in the genetic algorithm implementation:

• int *duplicate_gene(int *single_gene, int m) - given a single_gene and its length, this function duplicates the single gene. In other words, it allocates an int * array of length m using malloc, copies over the values from the single_gene into the new array, and returns it. This function is similar to the strdup function we discussed in class and in lab.
• double compute_meal_value(wt_val_coef_t wt_val_coef, int *single_gene) - given a wt_val_coef structure and a single gene, this function returns the value of the single_gene. The function is discussed in detail above.
• void print_meal_names(int *single_gene, int m) - given a single_gene and its length, this function prints out the names of the meal items associated with the single_gene. We are not requiring that you use this function, but if you want to see the composition of the meal constructed by your genetic algorithm, you can use this function to see the results.

Your Implementation

Your implementation will consist of five core functions (not including auxiliary) functions. We have provided skeleton code for these functions, described below:

• int *mutate(random_t random, int *single_gene, int m, int prob) - given a random_t structure, a single gene sequence, the length of that gene, and a probability of mutation, this function performs mutation on a single gene with probability of mutation for each element equal to \(\frac{1}{prob}\).
• int *crossover_and_choose(random_t random, int *first_parent, int *second_parent, int m) - given a random_t structure, two parent gene_sequences, and the length of the parents, this function performs crossover and randomly chooses one child from the resulting two children to be placed into the next generation.
• gene_pool_t insert(gene_pool_t old_gene_pool, wt_val_coef_t wt_val_coef, double max_cal, int max_surv) - given the gene pool from the last generation, a wt_val_coef structure, and constraints for maximum calories per meal and maximum number of survivors, this function constructs a new generation and places chosen survivors into the new generation using insertion-sort.
• gene_pool_t reproduce(random_t random, gene_pool_t gene_pool) - given a random_t structure and a half-empty, post-insertion-sort gene pool, this function calls the crossover and mutation functions and places children gene sequences into the new generation until the new gene pool contains a full set of gene sequences.
• int *solve(random_t random, gene_pool_t gene_pool, wt_val_coef_t wt_val_coef, int num_gens, double max_cal, int max_surv) - given a random_t structure, an initial gene pool, a wt_val_coef structure, a number of generations to perform, and constraints for maximum calories per meal and maximum number of survivors per generation, this function iteratively performs the genetic algorithm for the specified number of generations and returns the maximum value gene. In other words, this function repeatedly calls insert and reproduce to execute the fitness function and breeding process for each generation. Note that your solve function should create a defensive copy of the initial gene pool and iteratively perform the genetic algorithm on the copy, thus preserving the initial state of the original gene pool.

Test Code

We have provided you with test code to test each core function of your implementation:

• void test_mutation - this function runs your mutation function using preset random values seeded from a file. If the output of your function does not match the expected output, the function will print an error message.

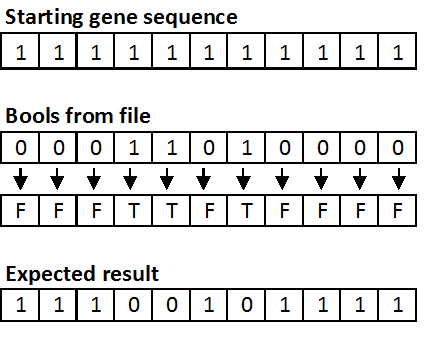
• void test_crossover_and_choose(int test_num) - this function runs your crossover function using preset random values seeded from a file. If the output of your function does not match the expected output, the function will print an error message.

• void test_insert(int test_num, double max_cal, int max_surv) - this function runs your insert function using preset random values seeded from a file. In particular, the function checks that the gene_pool returned is properly sorted (ie. sorted from highest to lowest solution values). If your code fails the test, this function will print out the values associated with each gene sequence in your gene_pool.
• void test_insert_from_file(int test_num, double max_cal, int max_surv) - this function runs your insert function using preset random values seeded from a file. In addition to testing whether or not your gene pool is properly sorted, the function checks whether or not the output of your code exactly matches the output of our solution. Again, if your code fails the test, this function will print out the values associated with each gene sequence in your gene_pool.

• void test_reproduce_from_file(int test_num) - this function runs your reproduce function using preset random values seeded from a file. If your code does not match the output of our solution, this function will print the non-matching gene_pools and an error message. If this function fails, check to be sure that you are drawing the parents properly from the post-insertion-sort gene_pool.

• void test_solve(int test_num) - this function seeds a random structure with values from a file and runs your solve function using these values. With the given set of random numbers, your code should return the following solution after 100 generations if working correctly:

This solution corresponds to a meal with: ROASTED GARLIC POTATOES, CARROT STICKS, GREEN BEANS, SEASONED SPINACH, CORNED BEEF WRAP, BAKED SWEET POTATO, CORN ON THE COB, and STEAMED FRESH BROCCOLI.

To run the test code, first run make. To run all of the test cases, simply run ./test_algorithm. To run a specific test case (there are a total of 6, index 0-5), run ./test_algorithm followed by the test number. For example, ./test_algorithm 3 would run the fourth test.

The test code is not comprehensive but will simplify the process of tracing errors.

Design Meetings

Design meetings are not required, but strongly encouraged. A design meeting form will be available soon. We will post a sign-up sheet for design meeting times on Piazza.

Submission

We will be using chisubmit for managing submission, including late chips. See Piazza for instructions regarding how to submit assignments and request late chips.

Acknowledgments: This assignment was designed by Trevor Coyle with help from Matthew Wachs and Anne Rogers.