Classes and Objects

Introduction

The goal of this lab is to understand how objects work, including how an application is designed following an object-oriented paradigm. In Lab 3, you wrote some functions of your own and got some practice calling them in order to create larger programs that were made possible through the composition of those functions. In this lab, you will take that idea a step further. You will use objects to organize and compose data in order to create a program that models a real-life dataset based on the 2013 Divvy Data Challenge.

Python is an object-oriented language, which means that everything in Python is really a structure called object. So, for example, when we create a string:

s = "Hello, world!"

What we’re really doing is creating an instance of the str class which we store in a variable called s. The “type of an object” is called its class. So, when we refer to “the str class” we refer to the specification of a datatype that is used to contain character strings.

In lecture, we’ve referred to some data types (like int and float as “primitive data types” that specify a domain of values (like integers, real numbers, boolean values, etc.). In Python, these data types are actually also objects, even if we don’t tend to think of them as such (in fact, some other programming languages, like Java, also handle primitive data types as non-object types). For example, if you create a float variable:

x = 0.33

Variable x is actually an instance of Python’s float class, which has a few handy methods, like as_integer_ratio, which returns the floating point number as a numerator/denominator tuple:

>>> x = 0.25
>>> x.as_integer_ratio()
(1, 4)

Play around with this type a bit. Notice anything interesting with certain floating point numbers?

In this lab, you will be able to get more practice working with classes. You will implement two classes of your own, and modify object-oriented code that we have prepared for you.

Working with the Divvy Data

As you probably know, Divvy is Chicago’s enormously popular bike sharing system. In 2014, Divvy published (anonymized) data on all the Divvy bicycle trips taken in 2013 (this data was published as part of the 2013 Divvy Data Challenge). The dataset contains two files: one with information about each Divvy station, and one with information about each Divvy trip.

In this lab, we will be focusing on the location data included with each station. Since each trip includes an origin station and a destination station, it is possible to compute an approximation of the distance travelled by a bike in a single trip (we can only compute the distance “as the crow flies”; the actual distance travelled is likely larger).

We will do this in two parts:

1. First, you will implement a Coordinates class that represents a location on Earth (specified by a longitude and a latitude). This class will include a method to compute the distance between two coordinates.
2. Next, you will edit a series of classes we have implemented that assume that the Coordinates class has been correctly implemented. More specifically, you will implement a series of methods that will ultimately allow you to compute the total distance of all the Divvy trips (and the average distance of each trip), and the average duration of each trip.

To get started, open up a terminal and navigate (cd) to your cs121-aut-16-username directory. Run git pull upstream master to collect the lab materials and git pull to sync with your personal repository.

Implementing a Coordinates class

One way of specifying a location on Earth is using longitude and latitude. From a programming perspective, using this representation means working with two floats. However, instead of always using two variables whenever we want to work with a longitude/latitude pair, we can define a new class called Coordinates that encapsulates all the functionality related to working with longitude/latitude coordinates.

The latitude and longitude in a Coordinates object should not change once you create the object. We would like you to use properties to declare that the latitude and longitude attributes are “read only.”

In this part of the lab, you will work with the following files:

• coordinates.py contains the skeleton of a Coordinates class. You will be editing this file.
• example_coordinates.py is an example program that creates and uses a Coordinates object, that is, an instance of the Coordinates class. You are not required to edit this file, but you are welcome to do so it if you’d like to experiment with your Coordinates implementation.
• test_coordinates.py is a test suite (for use with py.test) that will check whether your Coordinates implementation is correct. You should not edit this file.

You should do the following:

1. Implement the Coordinates constructor.
2. Define properties for latitude and longitude using the @property decorator. These attributes should be read-only, so you should not define setters for them.
3. Implement the distance_to method. This method must compute the distance between two coordinates (i.e., two longitude/latitude pairs) using the haversine formula:

\[2 r \arcsin\left(\sqrt{\sin^2\left(\frac{x_{lat} - y_{lat}}{2}\right) + \cos(y_{lat}) \cos(x_{lat})\sin^2\left(\frac{x_{long} - y_{long}}{2}\right)}\right)\]

where:

• \(x_{lat}, x_{long}\) is the latitude and longitude in radians of point \(x\).
• \(y_{lat}, y_{long}\) is the latitude and longitude in radians of point \(y\).
• \(r\) is the radius of the sphere. Note: The average radius of Earth is 6,371km. Your implementation only needs to work with Earth-sized spheres, so you can hard-code the value of Earth’s radius in your formula.

Note that you will need to convert the coordinate’s latitude and longitude from degrees to radians. The Python math library contains the necessary trigonometric functions and a function that converts a floating point value from degrees to radians. You can figure out how to use these functions by looking at the library’s API.

3. Implement the __str__ method. Having this method will make the output of the examples easier to read and verify, but is not strictly necessary. Your implementation can be as simple as printing the latitude followed by the longitude (separated by a comma). If you want to include cardinal points (that is, N, S, E, or W), negative latitudes are South and positive latitudes are North, and negative longitudes are West and positive longitudes are East.

Testing your Coordinates implementation

You can quickly test your implementation by running example_coordinates.py class:

python3 example_coordinates.py

A correct implementation should print the following:

The coordinates of Chicago are (41.834 N, 87.732 W)
The coordinates of New York are (40.706 N, 73.978 W)
The distance between Chicago and New York is 1155.08km

Note that the exact format of the coordinates may vary depending on your implementation of the __str__ method. However, the values themselves should be the same as shown above (although not necessarily with the same precision). The distance should also be the same as shown above.

You can run a more thorough set of tests using py.test and test_coordinates.py:

py.test -v -x test_coordinates.py

The output of this command will indicate whether you passed or failed the tests. Using the -x flag will cause py.test to stop running tests after the first failed test.

The Divvy Classes

In the remainder of the lab, you will be working with three classes that model the Divvy dataset:

• DivvyStation: A class representing an individual Divvy station.
• DivvyTrip: A class representing an individual Divvy trip.
• DivvyData: A class representing the entire dataset, which includes a list of stations and a list of trips.

An important aspect of object orientation is the ability to create relationships between different classes, to model real-world relationships. For example, a Divvy trip has an origin station and a destination station. Instead of trying to pack all the information about the stations in the DivvyTrip class, we instead have a separate DivvyStation class that is used to represent individual stations. The DivvyTrip class then only needs to have two attributes of type DivvyStation: one for the origin station and one for the destination station.

All the relations between the Divvy classes are summarized in the following figure:

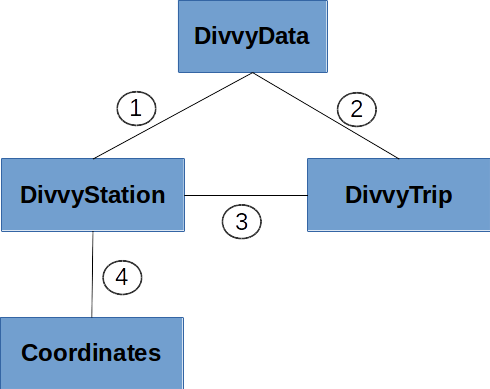
1,2. The DivvyData class represents the entire Divvy dataset, so it

contains a dictionary that maps station identifiers to DivvyStation objects and a list of DivvyTrip objects.

3. As discussed above, a DivvyTrip has two DivvyStation objects associated with it. This representation is implemented simply by setting two attributes, from_station and to_station in the DivvyStation constructor.
4. Finally, each Divvy station has a location, which we represent using an instance of the Coordinates class. Again, this is done simply setting an attribute, coords to a Coordinates object in the DivvyStation constructor.

When learning about object orientation, one common point of confusion is the difference between classes and objects. As we discussed earlier (in the introduction), a class is the specification of a datatype and an object is a specific instance of that datatype. So, if our Divvy dataset had three stations and five trips, we would have three DivvyStation objects and five DivvyTrip objects. We would additionally have three Coordinates objects (one for each DivvyStation object), because each station has a unique set of coordinates.

The figure below shows one possible way these object could be related amongst themselves (blue lines represent an “origin station” relation and green lines represent a “destination station” relation):

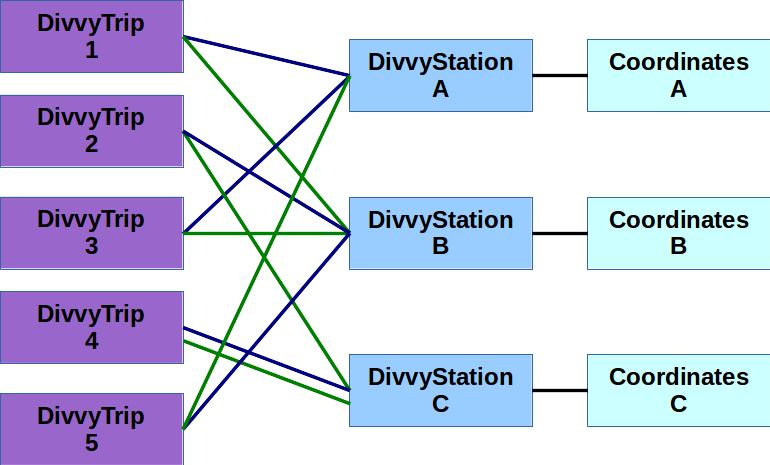
Notice how the DivvyStation objects are “shared” between the various DivvyTrip objects, and how it is even possible for a trip to have the same DivvyStation object as its origin and its destination.

One thing missing from the figure is the DivvyData object: during a run of any program using the Divvy classes, there will be a single DivvyData object containing all the trips and stations. In the example above, the DivvyData object would have a dictionary with the three DivvyStation objects, and a list with the five DivvyTrip objects.

Computing the Total Duration and Distance of all Trips

Given the Coordinates class and the Divvy classes, let’s say we wanted to compute the total distance of all the trips taken in 2013. We would need to do the following:

1. Add up the distance of each individual trip. The DivvyData class is where all the trips are located, so this seems like the logical place to implement this computation. However, to do this computation, we also need to...
2. Compute the distance for an individual trip. The DivvyTrip class represents the information for a single trip, so this class seems like the right place to implement this computation. However, take into account that a DivvyTrip object doesn’t contain the origin and destination coordinates directly. Those are contained in the origin and destination stations, which are represented by DivvyStation objects in the DivvyTrip object. However, once we have those stations (and their coordinates), we also need to...
3. Compute the distance between two geographical coordinates. Fortunately, we already implemented this function in the first part of the lab.

So, computing the total distance requires every class to pitch in with some functionality. This organization is a key aspect of object-orientation: encapsulation. Each class encapsulates the data and functionality of a specific “thing”.

In terms of specific code, you will need to do the following:

1. Implement the get_total_distance method in DivvyData.
2. Implement the get_distance method in DivvyTrip.
3. Use the coords attribute from DivvyStation to gain access to the coordinates.

Computing the total duration of all the trips is done similarly by implementing get_total_duration in DivvyData (the get_duration method in DivvyTrip is already provided, since it is trivial to implement).

Notice how this encapsulation and separation of concerns makes these objects easily composable: we implemented the Coordinates class before we knew about the Divvy classes but, once we have a working Coordinates class, we can just “plug it in” so the get_distance method in DivvyTrip can use it. Encapsulation also makes classes very easy to test: we were able to test the Coordinates class independently of how it was going to be used in the Divvy classes.

This task does not require much code and the code it does require is not complex. Our implementation is only 15-20 lines. The challenge, instead, is to understand how the pieces fit together and what that means for how to distribute the work of this task among the classes.

Testing your implementation

We have provided test code for your DivvyData class in the file test_divvy_data.py. To run the tests, run the command:

py.test -v -x test_divvy_data.py

The output of this command will indicate whether you passed or failed the tests. Using the -x flag will cause py.test to stop after the first failed test.

Designing your own class

Now that you’ve completed the implementation of several classes we’ve given you, now it is time for you to design a new class on your own. The goal is for you to implement a Route class representing a sequence of GPS coordinates, where each GPS coordinate includes a latitude, longitude, and an elevation. Your implementation of the Route class must include the following:

• A Route constructor that creates an empty route (i.e., with no coordinates/elevations).
• An append_GPS_coordinate method which adds a new GPS coordinate to the end of the route. If starting with an empty route, the first call to this method specifies the first GPS coordinate of the route.
• A get_total_distance method which computes the total distance of the route (adding up the distance between each point).
• A get_max_elevation_change method that computes the maximum absolute elevation change between any consecutive pair of coordinates in the route.

The internal details of the class, including the internal representation of the coordinates, and the parameters and return values of the methods is up to you. The only restrictions you have are that: (1) you must use the Coordinates class and (2) you cannot modify the Coordinates class, as any changes you make might break your solution to the Divvy classes.

Finally, because we don’t know the exact design of your solution, we cannot provide you with tests for this part of the lab. We encourage you to write test code for your implementation. In particular, if you create a route with the following coordinates:

	Latitude	Longitude	Elevation
1	41.79218	-87.599934	0.0
2	41.7902836	-87.5991959	10.0
3	41.791218	-87.601026	50.0
4	41.787965	-87.599642	40.0

The total distance should be 782.9397 and the maximum elevation change should be 40.0.

When Finished

When finished with the lab please check in your work (assuming you are inside the lab directory):

git add coordinates.py
git add divvy_trip.py
git add divvy_data.py
git add route.py
git add name_of_your_test_route_file.py
git commit -m "Finished with lab5"
git push

No, we’re not grading this, we just want to look for common errors.