Decision Trees

Due: Tuesday, March 1st at 5pm

The purpose of this assignment is to give you experience with data cleaning and decision trees.

You can work alone or in a pair on this assignment.

Getting started

Follow these start-up instructions if you plan to work alone.

Follow these start-up instructions if you are going to work with a previous CS122 partner.

Follow these start-up instructions if you are going to work with a new partner.

Once you follow these instructions, your repository will contain a directory named pa5. That directory will include:

• transform.py: skeleton code for Task 1.
• decision_tree.py: skeleton code for Task 2.
• data: a directory with sample data sets.

Pima Indian Data

The Pima Indian Data Set, which is from the UC Irvine Machine Learning Repository, contains anonymized information on women from the Pima Indian Tribe. This information was collected by the National Institute of Diabetes and Digestive and Kidney Diseases to study diabetes, which is prevalent among members of this tribe.

The data set has 768 entries, each of which contains the following attributes:

1. Number of pregnancies
2. Plasma glucose concentration from a 2 hours in an oral glucose tolerance test
3. Diastolic blood pressure (mm Hg)
4. Triceps skin fold thickness (mm)
5. 2-Hour serum insulin (mu U/ml)
6. Body mass index (weight in kg/(height in m)^2)
7. Diabetes pedigree function
8. Age (years)
9. Has diabetes (1 means yes, 0 means no)

Task 1: Data Cleaning

Your first task is to clean and then transform the raw Pima data into a training set and a testing set.

We have seeded your pa5 directory with a file named transform.py. This file includes code for a main function that takes three file names as arguments: (1) the name of a raw Pima data file, (2) a filename for the training data, and (3) a filename for the testing data. You must add code to clean and transform the raw data as described below and to generate CSV files with training and testing data.

Each row in the raw file contains an observation. The raw attribute values are floating point numbers. For every attribute but the first and the last, a zero should be interpreted as missing data. The fourth and fifth columns have a lot of missing data, so you should eliminate them when you process the data. Also, you should remove any observation that has a plasma glucose concentration, diastolic blood pressure, or body mass index of zero.

Once the data is cleaned, you will need to convert the numeric data into categorical data. For each category, we provide a list of triples. Given a triple, (l, lb, ub), a value x should be assigned label l if lb <= x < ub. Notice that the lower bound is inclusive and the upper bound is exclusive. The python expression float('inf') evaluates to positive infinity. For all floating point values x, x < float('inf').

• Pregnant: [("low", 0, 2), ("medium", 2, 6), ("high", 6, float('inf'))]
• Plasma glucose: [("low", 0.1, 95), ("medium", 95, 141), ("high", 141, float('inf'))]
• Diastolic blood pressure: [("normal", 0.1, 80), ("pre-hypertension", 80, 90), ("high", 90, float('inf'))]
• Body mass index: [("low", 0.1, 18.5), ("healthy", 18.5, 25.1), ("overweight", 25.1, 30.1), ("obese", 30.1, 35.1), ("severely-obese", 35.1, float('inf))]
• Diabetes pedigree function: [("low", 0.1, 0.42), ("medium", 0.42, 0.82), ("high", 0.82, float('inf'))]
• Age: [("r1", 0.1, 41), ("r2", 41, 60), ("r3", 60, float('inf'))]

Finally, once the data is cleaned and transformed, you should randomly split the observations into two sets: training and testing. The training set should contain roughly 90% of the transformed data, with the remainder going into the testing set.

The raw data includes a header row, which should be suitably modified and included in both output files.

Decision Trees

As we discussed in lecture, decision trees are a data structure used to solve classification problems. Here is a sample decision tree that labels tax payers as potential cheaters or non-cheaters.

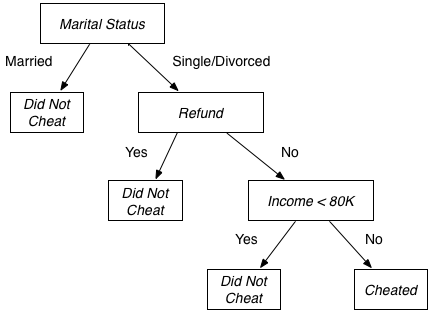
This tree, for example, would classify a single person who did not get a refund and makes $85,000 a year as a possible cheater.

We briefly summarize the algorithm for building decision trees below. See the chapter on Classification and Decision Trees from Introduction to Data Mining by Tan, Steinbach, and Kumar for a more detailed description.

Definitions

Before we describe the decision tree algorithm, we need to define a few formulas. Let \(S\) be a multiset of observations and \(A\) be an attribute.

We use the following definitions:

\[\begin{split}S_{A=j} & = & \{r \in S \, \lvert \, r[A] = j\} \\ \\ p(S, A, j) & = & \frac{\lvert S_{A=j} \rvert}{\lvert S \rvert} \\\end{split}\]

to describe the subset of the observations in \(S\) that have value j for attribute \(A\) and the fraction of the observations in \(S\) that have value j for attribute \(A\).

Decision Tree Algorithm

Given a multiset of observations \(S\) a target attribute \(T\), (that is, the label we are trying to predict) and a set, \(ATTR\), of possible attributes to split on, the basic decision tree algorithm works as follows:

1. Create a tree node, N, with its class set to the value that occurs most often:

\[\DeclareMathOperator*{\argmax}{arg\!max}\]\[\argmax\limits_{v \in values(T)} \, p(S, T, v)\]

where \(values(T)\) is the set of possible values for attribute \(T\).

2. If all the observations in \(S\) are from the same class, \(ATTR\) is the empty set, or the remaining observations share the same values for the attributes in \(ATTR\), return the node N.
3. Find the attribute \(A\) from \(ATTR\) that yields the largest gain ratio (defined below), set the split attribute for tree node N to be \(A\),and set the children of N to be decision trees computed from the subsets obtained by splitting \(S\) on \(A\) with T as the target class, and ATTR - A as the set of possible split attributes. The edge from N to the child computed from the subset \(S_{A=j}\) should be labeled \(j\). Stop the recursion if the largest gain ratio is zero.

We will use the gini coefficient to measure impurity:

\[gini(S, A) = 1 - \Sigma_{j \in values(A)} \; p(S, A, j)^2\]

We use the term gain to describe the increase in purity with respect to attribute \(T\) that can be obtained by splitting the observations in \(S\) according to the value of attribute \(A\). It is defined formally as:

\[gain(S, A, T) = gini(S, T) \, - \sum\limits_{j \in values(A)} p(S, A, j) * gini(S_{A=j}, T)\]

We might see a large gain merely because splitting on an attribute produces many small subsets. To protect against this problem, we will compute a ratio of the gain from splitting on an attribute to a value known as the split information for that attribute:

\[gain\_ratio(S, A, T) = \frac{gain(S, A, T)}{split\_info(S, A)}\]

where split information is defined as:

\[split\_info(S, A) = - (\sum\limits_{j \in values(A)} p(S, A, j) * log \, p(S, A, j))\]

Task 2: Building and using decision trees

We have seeded your pa5 directory with a file named decision_tree.py. This file includes a main function that processes the expected command-line arguments–filenames for the training and testing data–and then calls a function named go. Your task is to implement go and any necessary auxiliary functions. go should build a decision tree from the training data and then return a list of the classifications obtained by using the decision tree to classify the observations in the testing data.

Your program must be able to handle any data set that (1) has a header row, (2) has categorical attributes, and (3) in which the (binary) target attribute appears in the last column. You should use all the columns except the last one as attributes. We recommend using the column numbers in place of the column names in \(ATTR\) and for \(T\).

You could break ties in steps 1 and 3 of the algorithm arbitrarily, but to simplify the process of testing your code we will specify a specific method: break ties in step 1 by choosing the value that occurs earlier in the natural order for strings and in step 2 by choosing the attribute with the smaller column number.

Submission

Follow these submission instructions if you are working alone.

Follow these submission instructions if you are working in a pair.