Homework 7 (0 points)

Download the skeleton file ArrayList.elm.

Problem 1: Random Access Lists

Chapter 9.2.1 describes how to implement purely functional arrays with fast (O(log n)) random access (to get and set).

First, we define a binary leaf tree to be a binary tree that contains data only at the leaves (nodes with zero children):

type alias Rank = Int
type LeafTree a = Leaf a | Branch Rank (LeafTree a) (LeafTree a)

A complete binary tree of rank r is a binary leaf tree with height r + 1 and 2^r leaves. Alternatively, a complete binary tree of rank 0 is a leaf, and a complete binary tree of rank r is a branch with two complete binary tree children of rank r − 1.

For example:

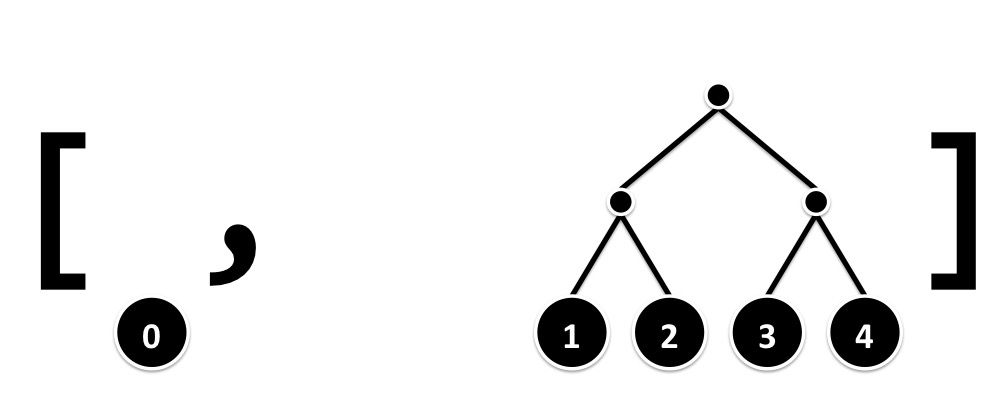
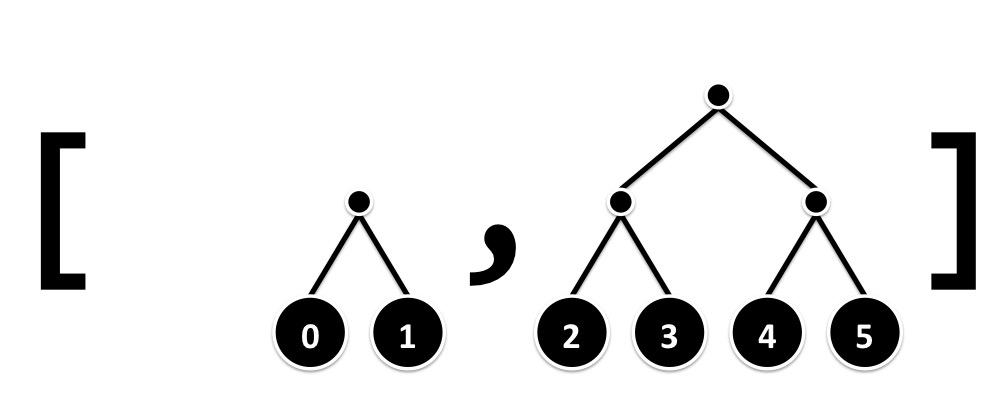
Second, we use complete binary leaf trees to represent arbitrary numbers of elements. Any number n of values can be represented with a list of at most ⌊log(n + 1)⌋ complete binary leaf trees, with at most one tree each of rank 0 to ⌊log(n)⌋.

We define the type below to capture this representation. For all operations that create and manipulate List (LeafTree a) values, we assume that the ranks are in strictly increasing order.

type ArrayList a = ArrayList (List (LeafTree a))

For example, the following three pictures show the representations of the 5 numbers 0 to 4 (left), the 6 numbers 0 to 5 (middle), and the 7 numbers 0 to 6 (right).

You may find the following helper function useful (or maybe not):

rank : LeafTree a -> Int
rank t =
  case t of
    Leaf _       -> 0
    Branch r _ _ -> r

7.1.1 --- Okasaki, Exercise 9.3

Implement the helper function...

consTree : LeafTree a -> List (LeafTree a) -> List (LeafTree a)

... so that it can be used to implement the cons operation.

cons : a -> ArrayList a -> ArrayList a
cons x (ArrayList trees) =
  ArrayList (consTree (Leaf x) trees)

The consTree function should run in O(log(n)) time. Your solution can assume that the only call to consTree is in cons as above.

7.1.2 --- Okasaki, Exercise 9.3 (continued)

When the first element is removed from a complete binary leaf tree of rank r, the remaining elements form r complete binary leaf trees with ranks 0 to r − 1. Implement this functionality in

splitTree : LeafTree a -> (a, List (LeafTree a))

such that splitTree can be used to define head and tail as follows.

head : ArrayList a -> Maybe a
head (ArrayList trees) =
  case trees of
    [] ->
      Nothing
    t::rest ->
      let (x, ts) = splitTree t in
      Just x

tail : ArrayList a -> Maybe (ArrayList a)
tail (ArrayList trees) =
  case trees of
    [] ->
      Nothing
    t::rest ->
      let (x, ts) = splitTree t in
      Just (ArrayList (ts ++ rest))

Your splitTree function should run in O(log²(n)) time. Better yet, it should run in O(log(n)) time, but this is not required.

7.1.3 --- Okasaki, Exercise 9.3 (continued)

Implement the get function

get : Int -> ArrayList a -> Maybe a

to retrieve the element at the given 0-based index, running in O(log(n)) time. If the index is out bounds, return Nothing.

Hints: Your solution needs to (i) find the appropriate LeafTree and (ii) find the appropriate Leaf within that LeafTree. The functions (^), (//), and (-) may be helpful.

7.1.4 --- Okasaki, Exercise 9.3 (continued)

Implement the set function

set : Int -> a -> ArrayList a -> Maybe (ArrayList a)