Red-Black Trees

Red-black trees are binary search ordered trees that are roughly balanced, resulting in O(log n) membership, insertion, and deletion operations. The code for this lecture can be found in RedBlackTree.elm.

All non-empty nodes in a red-black tree are colored red or black.

type Color  = R | B
type Tree a = E | T Color (Tree a) a (Tree a)

By convention, we will draw square boxes for Black nodes and round circles for Red nodes:

We define height and size of trees as before:

height t =
  case t of
    E         -> 0
    T _ l _ r -> 1 + max (height l) (height r)

size t =
  case t of
    E         -> 0
    T _ l _ r -> 1 + size l + size r

Invariants

A tree t is a valid red-black tree if:

0. t satisfies the binary search order property. That is, bso t == True, where

   bso t =
     let
       nonDecreasing xs =
         case xs of
           x1::x2::rest -> x1 <= x2 && nonDecreasing (x2::rest)
           _            -> True
     in
     nonDecreasing (toList t)
   
   toList : Tree a -> List a
   toList t =
     case t of
       E ->
         []
       T _ left x right ->
         toList left ++ [x] ++ toList right

1. No red node in t has a red child. That is, noRedRed t == True, where

   noRedRed t =
     case t of
       E                   -> True
       T R (T R _ _ _) _ _ -> False
       T R _ _ (T R _ _ _) -> False
       T _ l _ r           -> noRedRed l && noRedRed r

2. Every path from the root of t to a leaf contains the same number of black nodes. That is, okBlackHeight t == True, where

   okBlackHeight t =
     case maybeBlackHeight t of
       Just _  -> True
       Nothing -> False
   
   maybeBlackHeight t =
     case t of
       E ->
         Just 0
       T c l _ r ->
         maybeBlackHeight l |> Maybe.andThen (\n ->
         maybeBlackHeight r |> Maybe.andThen (\m ->
           if n /= m then Nothing
           else if c == B then Just (1 + n)
           else Just n
         ))

   Note that E nodes are not counted in path lengths. When maybeBlackHeight t == Just n, we refer to n as the black height of t.

   blackHeight t =
     case maybeBlackHeight t of
       Just n  -> n
       Nothing -> Debug.todo "blackHeight E"

To summarize the invariants:

redBlackTree t =
  bso t && noRedRed t && okBlackHeight t

(Some presentations additionally require the root of a red-black tree to be black. We omit this requirement here, as it is not necessary to achieve the desired balance property, below.)

Balance Property

A consequence of the noRedRed invariant is that the longest path from root to leaf in a red-black tree is one that starts and ends with red and alternates between red and black in between. The shortest path is one that consists only of black nodes. Because of the okBlackHeight invariant, the number of black nodes on the shortest and longest paths is equal. Therefore, the longest path in a red-black tree (i.e. its height) is at most twice the length of the shortest path (i.e. its black height). Specifically:

• [Max Height] ∀t. redBlackTree t ⇒ height t ≤ (2 * blackHeight t) + 1

In-Class Exercise. Prove:

• [Min Size] ∀t. redBlackTree t ⇒ size t ≥ 2^(blackHeight t) - 1
• [Balance] ∀t. redBlackTree t ⇒ height t ≤ 2(log(1 + size t)) + 1

Thus, the height of a red-black tree t of size n is O(log n).

Membership

Finding an element in a red-black tree proceeds just like finding an element in an arbitrary binary search tree (cf. findBST).

member : comparable -> Tree comparable -> Bool
member x t =
  case t of
    E ->
      False
    T _ l y r ->
      if x == y then True
      else if x < y then member x l
      else member x r

Insertion

The insertion procedure we saw earlier (cf. insert for BSTs) walks down a path in the tree making left and right turns as necessary according to the order property. Then, if the element is found nowhere in the tree, it is added as a leaf. Even when the input binary search tree is balanced, the resulting tree will generally not be.

One approach would be to add a black node at this final position, satisfying the noRedRed invariant but violating the okBlackHeight property. Another approach is to add a red node at this final position, satisfying the okBlackHeight property but violating noRedRed.

The idea behind the insertion algorithm is to start with the latter approach --- coloring the new node red, possibly resulting in temporary red-red violation --- and then to walk back up the search path fixing and propagating any violations upwards. The algorithm maintains the invariant that at most one red-red violation is allowed at a time.

The ins function walks down the search path, inserts a red node as the new leaf, and (after the recursive calls finish) walks back up the search path calling balance to fix any temporary red-red violations.

ins : comparable -> Tree comparable -> Tree comparable
ins x t =
  case t of
    E ->
      T R E x E
    T color l y r ->
      if x == y then t
      else if x < y then balance color (ins x l) y r
      else balance color l y (ins x r)

The balance function looks for red-red violations, which can occur in one of four configurations. In each case, the solution is the same.

In code:

balance : Color -> Tree comparable -> comparable -> Tree comparable -> Tree comparable
balance color l val r =
  case (color, (l, val, r)) of
    (B, (T R (T R a x b) y c, z, d)) -> T R (T B a x b) y (T B c z d)
    (B, (T R a x (T R b y c), z, d)) -> T R (T B a x b) y (T B c z d)
    (B, (a, x, T R (T R b y c) z d)) -> T R (T B a x b) y (T B c z d)
    (B, (a, x, T R b y (T R c z d))) -> T R (T B a x b) y (T B c z d)
    _                                -> T color l val r

The balance function fixes a red-red violation when processing a black parent node that contains it. If ins propagates a red-red violation all the way up to the root, there is no call to balance to fix it. Therefore, the last step in the insertion algorithm is to color the new root node black — which has no effect if it already was black. (Alternatively, we could leave the root red if it has no red child.)

insert : comparable -> Tree comparable -> Tree comparable
insert x t =
  case ins x t of
    T _ l y r ->
      T B l y r
    E ->
      Debug.todo "insert"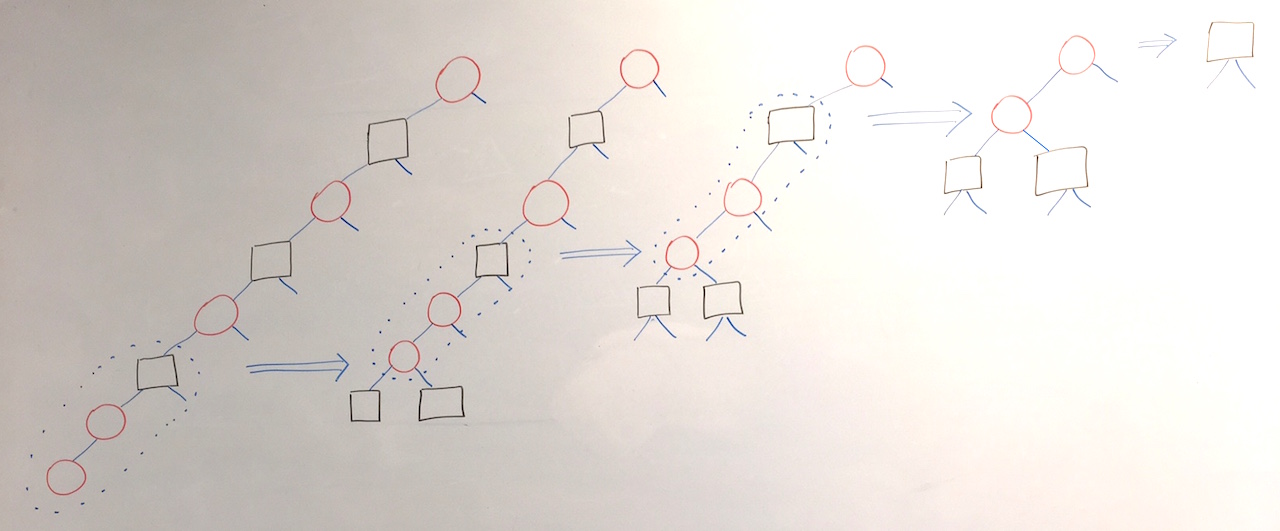

Exercise: Non-Empty Trees

The Debug.todo in insert is a bummer. Redefine ins/balance/insert to avoid it.

Deletion

See Homework 5, and the optional reading below.

Reading

Required

• Okasaki, Chapter 3.3

Optional

• Red Black Trees: Delete