Class Meeting 03: Robot State Estimation

Today's Class Meeting

Gaining familiarity with various approaches to robot state estimation (Bayes filters, Kalman filters, particle filters) - here's a link to today's slides
Completing a class exercise on state estimation

What You'll Need for Today's Class

You may find it helpful to have some scratch paper on hand to work through today's class exercises.

Groups for Today's Class

For today's class exercise, you'll be able to choose your own groups. Please get together in groups of 2-3 students.

Robot State Estimation

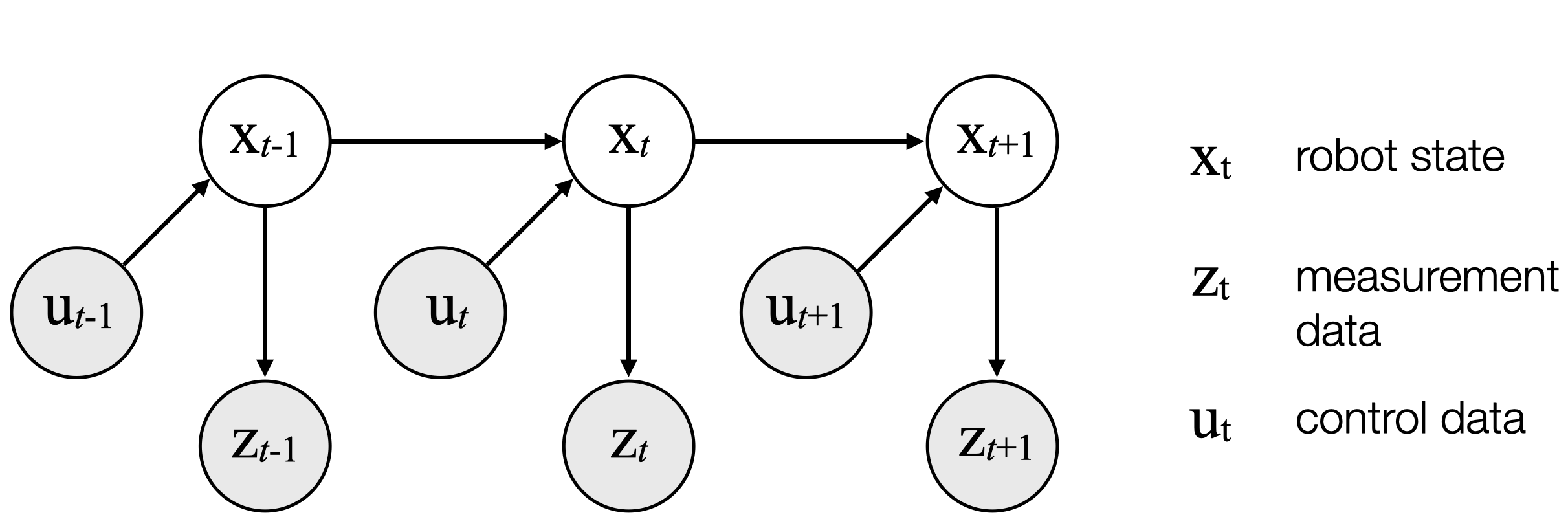
Today, we're covering topics related to how a robot estimates its state ($x_t$) using measurement data ($z_t$) and the knowledge of the actions the robot takes in the environment ($u_t$). This problem can be represented as a hidden Markov model or dynamic Bayes network as depicted in the following diagram.

Bayes Filter Algorithm

The following is the Bayes filter algorithm as we discussed during class:

$\textrm{Bayes_Filter}( bel(x_{t-1}), u_t, z_t):$
$\qquad \textrm{for} \: \textrm{all} \: x_t \: \textrm{do} $
$\qquad \qquad \overline{bel}(x_t) = \int p(x_t | u_t, x_{t-1}) \: bel(x_{t-1}) \: dx_{t-1}$
$\qquad \qquad bel(x_t) = \eta \: p(z_t | x_t) \: \overline{bel}(x_t) $
$ \qquad \textrm{endfor}$
$ \qquad \textrm{return} \: bel(x_t) $

Some useful tips/notes:

$\eta$ is a normalizer used to ensure that $\int_t bel(x_t) = 1$
When we compute the update rule, $\overline{bel}(x_t) = \int p(x_t | u_t, x_{t-1}) \: bel(x_{t-1}) \: dx_{t-1}$, for finite state spaces, the integral turns into a finite sum: $\overline{bel}(x_t) = \sum_{x_{t-1}} p(x_t | u_t, x_{t-1}) \: bel(x_{t-1}) $.

Class Exercise: Estimating the State of a Door (Bayes Filter Algorithm)

We'll first go over this as a class example and the belief calculation for $t = 1$ as a class.

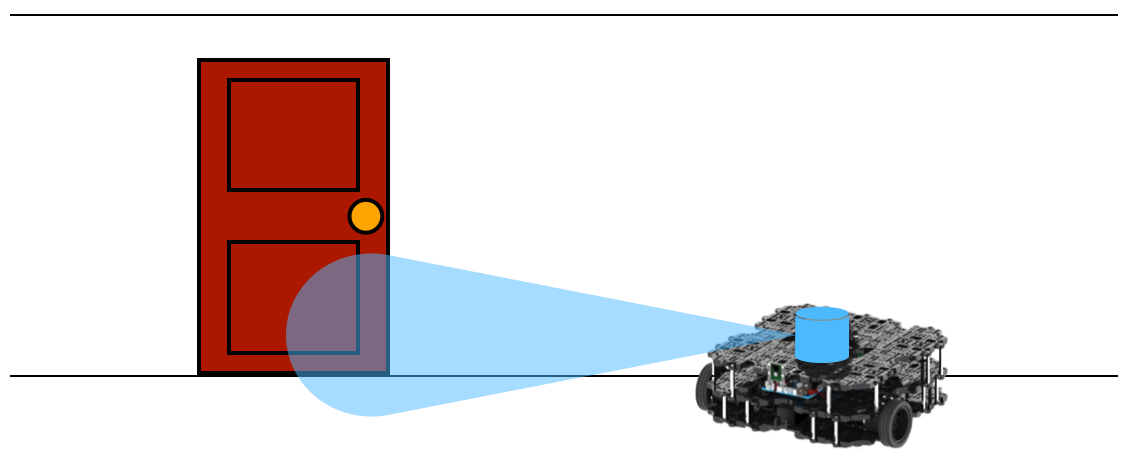
We'll practice applying the Bayes filter on a situation where a robot is estimating the state of a door using a forward-facing camera. We will assume that the door can be in one of two states: 1) open or 2) closed. Also, we'll assume that the robot doesn't know what state the door is in, so we assign a prior probability for the two states of: $$bel(X_0 = \textrm{open}) = 0.5$$ $$bel(X_0 = \textrm{closed}) = 0.5$$

Let's also assume that the robot's camera sensor is noisy and can be characterized by the following conditional probabilities: $$p(Z_t = \textrm{sense_open} \: | \: X_t = \textrm{is_open}) = 0.6$$ $$p(Z_t = \textrm{sense_closed} \: | \: X_t = \textrm{is_open}) = 0.4$$ $$p(Z_t = \textrm{sense_open} \: | \: X_t = \textrm{is_closed}) = 0.2$$ $$p(Z_t = \textrm{sense_closed} \: | \: X_t = \textrm{is_closed}) = 0.8$$ These probabilities indicate to us that the robot's sensors have less error when sensing when the door is closed (error = 0.2) than when sensing when the door is open (error = 0.4).

Our final set of assumptions are about the robot's ability to influence the environment. Let's assume that the robot can use its arm to push open the door with a 0.8 chance: $$p(X_t = \textrm{is_open} \: | \: U_t = \textrm{push}, X_{t-1} = \textrm{is_open}) = 1$$ $$p(X_t = \textrm{is_closed} \: | \: U_t = \textrm{push}, X_{t-1} = \textrm{is_open}) = 0$$ $$p(X_t = \textrm{is_open} \: | \: U_t = \textrm{push}, X_{t-1} = \textrm{is_closed}) = 0.8$$ $$p(X_t = \textrm{is_closed} \: | \: U_t = \textrm{push}, X_{t-1} = \textrm{is_closed}) = 0.2$$ If the robot decides not to open the door: $$p(X_t = \textrm{is_open} \: | \: U_t = \textrm{do_nothing}, X_{t-1} = \textrm{is_open}) = 1$$ $$p(X_t = \textrm{is_closed} \: | \: U_t = \textrm{do_nothing}, X_{t-1} = \textrm{is_open}) = 0$$ $$p(X_t = \textrm{is_open} \: | \: U_t = \textrm{do_nothing}, X_{t-1} = \textrm{is_closed}) = 0$$ $$p(X_t = \textrm{is_closed} \: | \: U_t = \textrm{do_nothing}, X_{t-1} = \textrm{is_closed}) = 1$$

Belief calculation for $t = 1$

Now, we are going to assume that the robot executes the action $u_1 = \textrm{do_nothing}$ and receives the measurement $z_1 = \textrm{sense_open}$ from its camera. We'll walk through this example and have you calculate the belief for the next time step ($t = 2$).

$\overline{bel}(x_1) = \int p(x_1 | u_1, x_{0}) \: bel(x_{0}) \: dx_{0}$
$\qquad \quad = \sum_{x_0} p(x_1 | u_1, x_{0}) \: bel(x_{0}) $
$\qquad \quad = p(x_1 | U_1 = \textrm{do_nothing}, X_0 = \textrm{is_open}) \: bel(X_0 = \textrm{is_open}) + $ $\qquad \qquad \: p(x_1 | U_1 = \textrm{do_nothing}, X_0 = \textrm{is_closed}) \: bel(X_0 = \textrm{is_closed}) $

Now, we can calculate $\overline{bel}(x_1)$ for both $X_1 = \textrm{is_open}$ and $X_1 = \textrm{is_closed}$.

$\overline{bel}(X_1 = \textrm{is_open}) = p(X_1 = \textrm{is_open} \: | \: U_1 = \textrm{do_nothing}, X_0 = \textrm{is_open}) \: bel(X_0 = \textrm{is_open}) + $
$\qquad \qquad \qquad \qquad \quad \: p(X_1 = \textrm{is_open} \: | \: U_1 = \textrm{do_nothing}, X_0 = \textrm{is_closed}) \: bel(X_0 = \textrm{is_closed}) $
$\qquad \qquad \qquad \qquad = 1 \cdot 0.5 + 0 \cdot 0.5 = 0.5 $

$\overline{bel}(X_1 = \textrm{is_closed}) = p(X_1 = \textrm{is_closed} \: | \: U_1 = \textrm{do_nothing}, X_0 = \textrm{is_open}) \: bel(X_0 = \textrm{is_open}) + $
$\qquad \qquad \qquad \qquad \quad \: \: \: p(X_1 = \textrm{is_closed} \: | \: U_1 = \textrm{do_nothing}, X_0 = \textrm{is_closed}) \: bel(X_0 = \textrm{is_closed}) $
$\qquad \qquad \qquad \qquad \: \: = 0 \cdot 0.5 + 1 \cdot 0.5 = 0.5$

It should not surprise us that $bel(X_0) = \overline{bel}(X_1) $, since the robot action $\textrm{do_nothing}$ does not influence the state of the world. Once we do the measurement update, however, our belief will change. Our belief update takes the form: $$bel(x_1) = \eta \: p(Z_1 = \textrm{sense_open} \: | \: x_1) \: \overline{bel}(x_1)$$

We have two possible resulting states, $X_1 = \textrm{is_open}$ and $X_1 = \textrm{is_closed}$:

$bel(X_1 = \textrm{is_open}) = \eta \: p(Z_1 = \textrm{sense_open} \: | \: X_1 = \textrm{is_open}) \: \overline{bel}(X_1 = \textrm{is_open}) $
$\qquad \qquad \qquad \quad \: \: \: \: = \eta \: 0.6 \cdot 0.5 = \eta \cdot 0.3 $

$bel(X_1 = \textrm{is_closed}) = \eta \: p(Z_1 = \textrm{sense_open} \: | \: X_1 = \textrm{is_closed}) \: \overline{bel}(X_1 = \textrm{is_closed}) $
$\qquad \qquad \qquad \qquad \: \: = \eta \: 0.2 \cdot 0.5 = \eta \cdot 0.1 $

We can now calculate the normalizer ($\eta$) so that $\sum bel(x_1) = 1$ :

$ \eta = (0.3 + 0.1)^{-1} = 2.5$

So, now our belief after time step 1 is:

$bel(X_1 = \textrm{is_open}) = 0.75 $
$bel(X_1 = \textrm{is_closed}) = 0.25 $

Belief calculation for $t = 2$

For the belief calculation for $t = 2$, work in groups of 2-3 students. You will likely find it hepful to use scratch paper or an equivalent.

For time step 2, we are going to assume that the robot executes the action $u_2 = \textrm{push}$ and receives the measurement $z_2 = \textrm{sense_open}$ from its camera. In your group, calculate $\overline{bel}(x_2)$ and $bel(x_2)$.

Once you finish calculating $\overline{bel}(x_2)$ and $bel(x_2)$ you can check your solutions on this door state estimation exercise solutions page.

Acknowledgments

The content and exercises for today's class were informed by Probabilistic Robotics by Sebastian Thrun, Wolfram Burgard, and Dieter Fox.