CMSC 22610
Implementation of Computer Languages - I
Winter 2009

1. Write regular expressions for the following languages:
   1. Strings over the alphabet {a,b,c} with exactly 2 bs.
   2. Strings over the alphabet {a,b,c} where the first a precedes any occurrence of b and the first b precedes any occurrence of c.
   3. Strings over the alphabet {0,1} that describe binary integers (with no leading zeros) that represent a value of the form 2ⁿ+1.
2. (a)-(c) Draw non-deterministic finite automatons (NFAs) that accept the languages in Problems 1(a)-(c).
3. The following RE describes binary numbers (either signed or unsigned and either integer or floating point):

   (-|ε) (0|1)+ (.(0|1)+)? (E(+|-|ε)(0|1)+)?

   (Unlike Problem 1(c), this RE accepts leading zeros.) Draw a non-deterministic finite automata (NFA) that accepts the same language as the above RE.
4. Consider the following NFA over the alphabet {a,b,c}: 
   
   
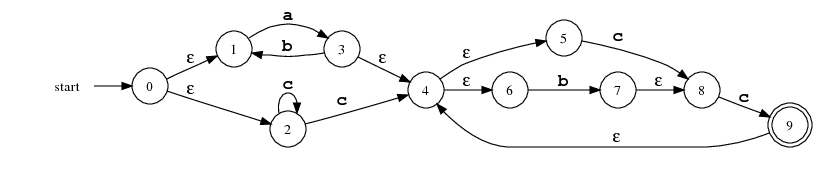
   1. Give the ε-closure for each state in the NFA.
   2. Convert the NFA to a DFA using the subset-construction method. (You may omit transitions to the error state (the DFA state corresponding to the empty set of NFA states).)
   3. Give an RE that defines the same language as the NFA.

Document history

January 27, 2009

Original version