Due Wednesday, April 6th, 11:59pm

Goals for this homework

  • Practice the C development cycle
  • Write a simple C program to get used to the syntax.
  • Write programs that exercise functions and control.

You are expected to complete this assignment individually. If you need help, you are invited to come to office hours and/or ask questions on piazza. Clarification questions about the assignments may be asked publicly. Once you have specific bugs related to your code, make the posts private.

This homework has several problems. We are also providing you with some resources on printf and error handling for this assignment.

Homework 1, which includes warmup 1, will be collected from your subversion repository on Wednesday, April 6th, at 11:59pm.

You should submit four files for this assignment (hw1.h, hw1.c, hw1_main.c, and Makefile) in your subversion repository as directed below. Your subversion repository is named CNET-cs152-win-16 and you can check it out with the following command: 

  $ svn checkout https://phoenixforge.cs.uchicago.edu/svn/CNET-cs152-win-16
(where CNET is your cnet). Do not commit any executable, a.out or any other, to your repository; we will (in fact, must) recompile your code on our own machines on our end.

printf

The printf() function takes a string as its first argument. The contents of this string are printed to the screen as-is, but with the same kinds of escape conventions as we saw in Racket (e.g., \n is the newline character). The function can be used with a string and no other parameters: 

  printf("Hello, world!\n");

If you want to include a representation of the value of one or more expression in the string printed by printf, you need to include one or more format codes in printf's string argument, and you need to pass correspondingly many expressions as additional arguments to printf, separated by commas. Some examples follow.

Format codes begin with the character % and the next character(s) specify the type of the value to be printed. For now, it suffices to know that d specifies an int, and lf specifies a double. To be clear, put together, we write %d as a placeholder when we want to write an int, %ld for a long int, and %lf for a double.

For example, 

  printf("The number is %d.\n", 42);
prints this: 
  The number is 42.

If we want more than one expression included in the same string, we use multiple format codes and pass arguments in lockstep with those codes: 

  int ndigits = 6;
  double approx_pi = 3.14159;
  printf("Pi to %d digits is %lf, and pi squared is %lf\n",
         ndigits, approx_pi, approx_pi * approx_pi);

Error Handling

Error handling capabilities vary by language, and what you want to do in an error varies by the situation. When an error occurs in a function, the question becomes, what should you do, and how do you notify the caller that an error occurred?

In C, there is no good way to distinguish error conditions from normal execution. This is a problem because if you write a function, and it's used in a variety of different circumstances, it is bad programming practice to determine within the function what will be done. For example, one program might want to exit, whereas another might want to notify the user that there was bad input and to try again.

In this course, we will print the error message in a special way (see below). If there is an opportunity, we will designate a specific return value for an error condition. If there is no available return value, then we will exit from within the function.

When we print error messages, it is helpful and appropriate for them to be routed through a special error mechanism. This gives them priority, increases their likelihood of being printed in the case of a program crash, and allows them to be separated from other output. To accomplish this, we use a variant of printf called fprintf. This function works the same as printf, but takes in an extra argument at the beginning: the "file" to which to write the message. Passing in stderr as that argument will send the output to the screen, but using the special error mechanism: 

  fprintf(stderr, "error: too many widgets for the number of grommets\n");
  fprintf(stderr, "error: need ten boondoggles, but only have %d\n", num_bds);

Sometimes, these lines will be followed by exit(1); This immediately exits the program and returns a code. If you were writing a large program, you might assign a different code to each type of error that would result in an exit.

Types

The homework problems follow. We use the type int for integers (except, in certain cases made explicit below, unsigned int), double for floating-point numbers (i.e., non-integers), and int for Booleans (noting that C has no Boolean type).

Makefile

Because you are adding a second set of files to your directory, you need to add a second target to your Makefile. In your makefile, add another two lines (with a space between these and the ones already there). 
hw1: hw1.h hw1.c hw1_main.c
	clang -Wall -o hw1 hw1.c hw1_main.c

Set Up

The first thing to do is to create a skeleton project that will minimally execute.
  • Step 1: Create hw1.h. Add prototypes for all functions in this assignment. For example: 
    double surface_area_cylinder(double height, double radius);
  • Step 2: Create hw1.c. For each function, implement the function with a single line - return with the right type. For example: 
    double surface_area_cylinder(double height, double radius)
{
	return 0.0;
}
  • Step 3: Create hw1_main.c. For each function, put in a single function call. For example: 
    int main()
{
	surface_area_cylinder(1.0, 5.0);
	// add the rest of the function calls here
}
First get this compiling and running. It won't print out anything, but this will mean that your code will compile and execute with our infrastructure. This must work in order to get any points in this course. Do this first, not last.

Problem 1

A cylinder is a three-dimensional shape that has a height and radius. Write the function surface_area_cylinder that takes in height and radius values, all doubles, in that order, and returns the outside surface area of the cylinder, a double. In other words, calculate the total area of all of its faces or sides, but only on the outside of the cylinder, not the inside.

The function header must be as follows: 

double surface_area_cylinder(double height, double radius);

If the user enters a negative number for any of the inputs, print out an error "error (area_cylinder): [description of error]". Remember, as described above, to use fprintf rather than printf and send the output to stderr. Return -1.0 to indicate that a negative input was received. Do not exit.

Don't forget to complete this portion, test it, and commit it before moving on!

Problem 2

/* print out a number in base 10, digit by digit */

Every character has an ASCII value. This means that 'a' has one value, 'b' another, 'A', another, '0' another, and so on. The exact numbers can be found in an ASCII table. These mappings of character to number are not random, but laid out specially so that you can perform useful math on them. As you probably learned from the warmup, 'a' + 5 is 'f'. Likewise, 'A' + 5 is 'F', and '0' + 5 is '5'.

Using this knowledge, use arithmetic on characters to print out the digits of a number, character by character. The only printf statement allowed is:

printf("%c",ch);

First write a function that prints out a single digit:

The function header must be as follows: 

void print_digit(unsigned int digit);

Then write a function that prints out an entire number, one digit at a time: 
void print_number(unsigned int number);
Note: You may not use an array for this problem. You must use recusion. Remember that recursion is a problem-solving technique, not just a solution.

You must clearly label your base case, smaller case, and general case

Don't forget to complete this portion, test it, and commit it before moving on!

Problem 3

A digit, such as 7, can be written as an English word, such as "seven," and 79 as "seventy-nine." This word has a certain number of letters; in this case, five and twelve, respectively. Write a function, digit_letters that takes in a single number, no more than one digit, represented as an unsigned int, and returns the number of letters in its English word, an int.

If the user enters anything other than a single digit number, print out an error "error (digit_letters): [description of error]". Remember, as described above, to use fprintf rather than printf and send the output to stderr. Return -1 to indicate that an improper input was received.

Note: You may not use an array for this problem.

The function header must be as follows: 

int digit_letters(unsigned int digit);

Don't forget to complete this portion, test it, and commit it before moving on!

Problem 4

Create a function, number_letters that returns the number of letters a number with up to three digits. For example, while 7 can be written "seven," 27 would be written "twenty-seven." 127 would be written "one hundred twenty-seven." Count both the internal spaces (3 in this case, between one, hundred, and twenty-seven) and the dash (in twenty-seven).

The function header must be as follows: 

int number_letters(unsigned int number);

Note: You may not use an array for this problem.
Don't forget to complete this portion, test it, and commit it before moving on!

Problem 5

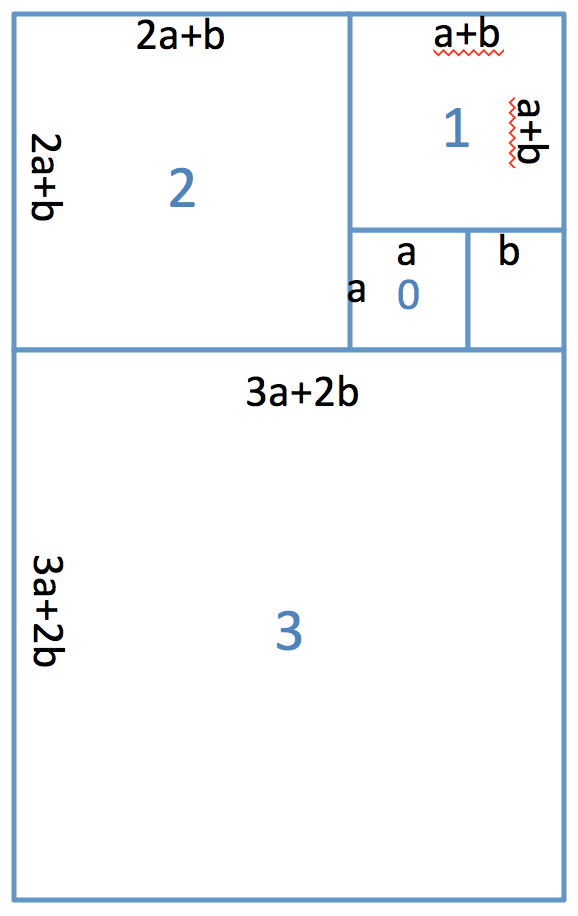
The Golden Spiral is a spiral based on the dimensions of the Golden Ratio, both which are found often in nature. For the golden ratio, we begin with a single box with length a. Then we place a rectangle next to it with the dimensions b, where (a + b) / a = a / b. If we solve this, then a/b = (1+sqrt(5))/2, or approximately 1.618.

One way to approximate the Golden Spiral is to add squares around the circle, with each square's length being the sum of the lengths of the two squares before it, as seen in the Fibonacci spiral on the above linked page. That means that, after the first rectangle of size axb is added, all subsequent additions are squares. In this case, a square of size (a+b)x(a+b) will be added, making a rectangle that is (a+b) x ((a+b)+a), and the next is (a+b+a) x ((a+b+a)+(a+b))

You are going to write a more generalized version of this process. Instead of requiring that a/b = 1.618, you are going to allow any arbitrary starting value for a and b. You will then calculate the dimensions of the subsequent squares that would be added on to create a structure like that in the pictures. Below is an image that illustrates the process for 3 squares.

Write a function that, given two starting values of a and b, calculates the length of the square that will be added after x applications of this ratio. In this case, the axa square is the 0th application, (a+b)x(a+b) is the 1st application, (a+b+a)x(a+b+a) is the 2nd application, and so on.

Here is the prototype for the function: 
float golden_spiral(float a, float b, int applications);

For this problem, you *must* use recursion. Remember to view recursion as a problem-solving technique rather than a solution.

Submit

At this point, you should have done the following:
  • Created four files and filled in the proper information: hw1.h, hw1.c, hw1_main.c inside your hw1 directory. 
  • $ svn add hw1.h hw1.c hw1_main.c
  • Implemented all of your functions. If not, you at least need skeletons of your functions so that our automated tests will compile for the functions you did write.
  • Compiled your executable manually and with the Makefile
  • Implemented your test cases
  • Executed your code
  • Debugged your code 
  • $ svn commit -m "hw1 complete"