Recursion¶
Introduction¶
The objective of this lab is to give you practice in writing and calling recursive functions.
Getting started¶
Open up a terminal and navigate (cd) to your
cmsc12100-aut-17-username directory, where username is your
CNetID. Run git pull upstream master to collect the directory for
this lab and git pull to sync with your personal repository.
The directory lab8 contains one file, named README.txt and
another named recursion.py. You will do all of your work for this
lab in recursion.py.
Quick review¶
Recursion is the concept of defining something by breaking it into similar, but smaller or simpler pieces. These smaller or simpler pieces are defined in the same way as the larger piece. Because of this, the definition “folds” or “wraps” in upon itself.
For example, consider the calculation of factorial. The factorial of an integer is the product of itself and each of the smaller integers, down to one. For instance:
We could write a loop to evaluate factorial:
def fact(n):
'''
Compute n!
'''
rv = 1
for k in range(1,n+1):
rv = rv * k
return rv
This is a non-recursive version of factorial.
But, we could also observe that we can break the calculation of factorial into a smaller case and then extend the result of the smaller case to the bigger one. In particular:
This approach allows us to write a recursive version, a version where the function calls itself:
def fact(n):
if n == 1:
return 1
return n*fact(n-1)
The last line is said to be the recursive case: the case where we call the same function again, but with a smaller input. The first case, the case where we are calculating the factorial of the number one, is called the base case, analogously to the base case in a proof by induction. This case is an exception to the general rule modeled by the recursive case. We do not want to calculate the factorial of one by referring to the factorial of a smaller number and possibly continuing the recursion down into the negative numbers. Instead, we want to define the value for this input as a hard-coded value with no further function calls.
Base cases are essential in recursion. They keep a recursive function from calling itself over and over again indefinitely. If a base case is missing, not only do we not get the correct answer, but we likely get no answer at all as the program attempts to recurse infinitely. When a recursive programs crashes or fails to complete a calculation, a missing base case is the likely culprit.
Part 1: Powers of two¶
If I give you a number, how can you tell if it is a power of two? (For this problem, we’re only going to consider non-negative, integer powers of two: 1, 2, 4, 8, …. We’re not talking about fractions, such as 1/2 or 1/4, or exponents that aren’t whole numbers.)
Here is a reasonable approach you might take: First, you might “eyeball” the number to see if you recognize it as a power of two; you have probably memorized many of the smaller such numbers over the years. Also, you might look for obvious clues that it is not a power of two (for instance, it is odd, and not one).
If those tactics did not yield an immediate answer, you might next refer to a logarithm table, or use a calculator to take a log. But suppose you don’t have these aids handy, or do not wish to pursue that approach.
You would then, probably, adopt a pencil-and-paper approach to determine if it was a power of two. This approach involves repeated calculations until you find evidence that the number is, or isn’t, a power of two.
Think about what those calculations would be, and how you can transform the question about a given number to one about a smaller number. (Hint: try to come up with an equation similar to the one we had for factorial.)
Task 1: Complete the function, is_power_of_two(n) in recursion.py.
In implementing this function, you may not use loops; that would defeat the purpose of practicing recursion.
Part 2: Fibonacci¶
We’ll next write a slightly more complex recursive function.
Try writing a recursive function to compute the Fibonacci numbers.
1, 1, 2, 3, 5, 8, 13, 21, 34, ....
The Fibonacci numbers may be mathematically defined as follows:
Or, in plain English, “Each number is the sum of the previous two numbers. The first two are both one.”
Task 2: Complete the function:
def fib(n):
That takes an integer n as its input and returns the nth
Fibonacci number. The above mathematical definition of Fibonacci numbers
can be expressed in terms of evaluations of this function:
>>> fib(0)
1
>>> fib(1)
1
>>> n = 7 # you can set n > 1, and the result should not change
>>> fib(n) == fib(n-1) + fib(n-2)
True
What is different about this function in relation to the other recursive functions we’ve seen? Roughly how many steps does this implementation of Fibonacci take to complete? Can you think of an aspect of how this function is implemented that is particularly inefficient?
Think about how many times the function fib(3) will be called in the evaluation of fib(5).
It will be called by fib(5) for the n-2 case, but it will also be called by fib(4) in the n-1 case.
Both of the times it is called, it calculates the result from scratch.
The function fib is the kind of function that should be expected to have the same output for the same input. But for both of the times fib(3) is called, it must be computed again. This problem is magnified as the value of n increases.
This type of function - one which always has the same result for the same input - is called pure. If a function is known to be pure, you can be more clever by storing its result in memory the first time it is calculated, and then referring to the cached result if it is needed in the future rather than recalculating it. If you take further computer science courses, you will explore this concept more extensively.
Part 3: Finding roots¶
You may have encountered Newton’s Method in a math class; it is an approach to finding the roots of a function (places where the function is zero, more precisely, \(x\)-values for which \(f(x) = 0\)). If this calculation does not sound extraordinarily useful in a wide variety of cases, keep in mind that you can rephrase the question “for what \(x\) is \(f(x)=y\)” into the question “for what \(x\) is \(f(x) - y = 0\)” simply by subtracting \(y\) from both sides of the equation, and then use Newton’s Method on the function \(g(x)\) where \(g(x)=f(x)-y\).
Here are a couple things you can do with this kind of algorithm:
- Compute the square root (cube root, or any root) of a number. The square root of \(7\), for instance, is a root of the function \(f(x) = x^2 - 7\)
- Compute inverse trigonometric functions. A root of \(f(x) = sin(x) - 0.5\) is an angle \(x\) for which \(sin(x) = 0.5\), also known as \(sin^{-1}(0.5)\).
One practical issue with Newton’s Method is that it uses the derivative of the function. We may not have an equation for the derivative, so we may prefer to use one of the variants of Newton’s Method that is simpler. These variants include (in order of complexity) the Bisection Method, the Secant Method, and the False Position Method.
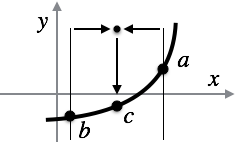
The Bisection Method begins with two \(x\)-values, \(a\) and \(b\), on either side of the root. In other words, \(f(a)\) and \(f(b)\) must have opposite signs. If the function \(f\) is continuous, then by the Intermediate Value Theorem, there must be an \(x\)-value between \(a\) and \(b\) such that \(f(x) = 0\). Put simply, the function has to pass through zero on its way between the negative value and the positive value.
However, we do not know where, between \(a\) and \(b\), this root might lie. But the Bisection Method simply tries the point \(c\), in the middle of \(a\) and \(b\), next.
There are a couple of possibilities at this point. First, \(c\) might actually be the root, or so close to it that we consider it close enough. In this case, we are done, and we call \(c\) the root. More likely, however, \(c\) is not close enough to the root. But, in that case, \(c\) is either positive or negative.
Think about how the problem of finding a root, now that we have evaluated \(f(c)\), has become a similar problem to the original problem of finding a root between \(a\) and \(b\). And why is this problem similar, but smaller?
What is the base case?
Ideally, our base case would be that \(f(c) = 0\). However, floating point calculations do not have perfect precision, and having a result that is exactly zero, with no error at all, is uncommon.
Thus, it is typical to use an “epsilon” value. (If you are not familiar with the practice, the Greek letter is commonly used to refer to a very small, but non-zero, value, that is considered “close enough.”) For instance, we might set \(epsilon = 0.001\) and accept any \(x\) for which \(-0.001 < f(x) < 0.001\).
So one way to stop the recursion is to find a \(c\) such that the absolute value of \(f(c)\) is less than a specified epsilon.
An alternative way is to stop when the difference between \(a\) and \(b\) becomes small. However, we will use the condition involving \(c\) and epsilon instead.
Task 3: Complete the function find_root_sqrt2 in recursion.py:
def find_root_sqrt2(epsilon, a, b):
that, for the function mentioned above that has a root at the square
root of two, returns the \(x\)-value of a root, or an
\(x\)-value for which the function assumes a value within
epsilon of zero. Place your implementation in recursion.py
Then, test your find_root_sqrt2 function with epsilon values of 1, 0.1, 0.01, and 0.001. Use a = 0.0 an b = 2.0 as starting points,
Here are some hints for debugging:
- You may want to print out the values of
a,b, andceach time the function is called. - You should be able to, using pencil and paper, apply the Bisection Method yourself. The values of \(a\), \(b\), and \(c\) for each step that you come up with should exactly match what your code is doing. If they do not, try to understand the source of the discrepancy.
- If your code always stops immediately in the base case without making even a single recursive call, modify your code to print out the value of
candepsilonand think about the test you are using to determine ifcmatches the base case. You might have forgotten something.
Task 4: Make a generalized version of your function, called find_root, that takes in a function f as a parameter as well (instead of always using the function with a root at the square root of two). To test your implementation, add two functions, root2 and sinPoint5, to recursion.py and then use them in a call to find_root. These functions should have roots at the square root of two, and an angle (in radians) at which the sin function assumes the value 0.5, respectively. For sinPoint5, use 0.0 and 1.0 as your starting points.
Part 4: Trees¶
Recursive functions are often used with recursively-defined data
structures. In this part, you will work with a recursively defined
tree. We will represent the nodes of the tree with a dictionary that
has three keys: key, which has a string as a value, val, which
has an integer as a value, and children, which has a list of tree
nodes as a value.
Here are a couple of example trees:
t0 = {"key":"node0",
"val":27,
"children":[]}
t1 = {"key":"node1",
"val":1,
"children":[{"key":"node2",
"val":2,
"children":[{"key":"node3",
"val":3,
"children":[]}]},
{"key":"node4",
"val":4,
"children":[]},
{"key":"node5",
"val":5,
"children":[]}]}
How would we define a function to compute the number of leaves (nodes with no children) in trees of this form? What is the base case? What are the recursive cases and how do we combine the results?
The recursion should stop when we hit a leaf, that is, when the input node has no children. If a node is not a leaf, then we need to compute the sum of the number of leaves in each of its children. Here is a straightforward translation of these requirements:
def count_leaves(t):
'''
Count the number of leaves in the tree rooted at t
Inputs: (dictionary) a tree
Returns: (integer) number of leaves in t
'''
assert t is not None
if not t["children"]:
return 1
num_leaves = 0
for kid in t["children"]:
num_leaves += count_leaves(kid)
return num_leaves
This function would return 1 when called with t0 and 3 when called
with t1.
Task 5: Complete the function:
def add_values(t):
which should take a tree node and return the sum of the values in the
tree rooted at that node. A call to add_values(t0) should return 27 and
a call to add_values(t1) should return 15.
Our implementation of this function is very similar to the previous function.
When Finished¶
When finished with the lab please check in your work (assuming you are inside the lab directory):
git add recursion.py
git commit -m "Finished with recursion lab"
git push
No, we’re not grading this, we just want to look for common errors.