Schelling’s Model of Housing Segregation (2017 edition)¶

Due: Friday, October 13th at 4pm

The goal of this assignment is to give you practice using nested loops, lists of lists, and functions.

You may work alone or in a pair on this assignment. The algorithms you need to implement for this assignment are more challenging than the first assignment. We recommend starting early.

Introduction¶

The New York Times has an interesting tool for viewing the distribution of racial and ethnic groups in cities and states around the country. If you look at the map for the Greater Chicago area, you will see that many areas are heavily segregated, but that some, such as the suburb of Glendale Heights, are not. The forces that led to this arrangement of people are complex and it is unlikely that any simple model can truly answer the questions of how segregation arises and why it persists. Keeping that in mind, one can still ask simple questions that may shed some light on the situation. In his 1978 book Micromotive and Macrobehavior, Thomas Schelling considered the following question: is it possible that a group of individuals would prefer to live in integrated neighborhoods and yet, as the result of their collective choices end up in segregated neighborhoods?

Schelling examined this question using a very simple model: A city has two kinds of people, Cubs fans and White Sox fans, for example, and each person in the city requires a certain number of his neighbors to be like him to feel comfortable in his location. Schelling used this model to study the patterns that emerge if, over time, people who are unsatisfied with their initial locations or become unsatisfied over time relocate to new locations that satisfy their criteria. What happens depends on the ratio of the two populations and on the satisfaction criteria used by the individuals, but segregation is a frequent outcome.

Your task in this assignment will be to implement a variant of Schelling’s model. Before you can do so, we need to specify the details of the model. In particular, we need to specify the:

shape and composition of a city,
boundaries of a home’s neighborhood,
definition for satisfaction,
rule for relocating unsatisfied homeowners,
composition of a step in the simulation, and
stopping conditions for the simulation.

Cities: A city is represented as an $N \times N$ grid (where the value of $N$ can be different for each city). Each grid location (or cell) represents a home, which can be in one of three states: open (that is, unoccupied), occupied by a red homeowner, or occupied by a blue homeowner. You can assume that a city has at least one open location.

In this assignment, you will always process the grid in row major order. That is, you will use a doubly-nested loop in which the index variable in the outer loop starts at zero and is used to indicate the current row, and the index variable in the inner loop starts at zero and is used to indicate the current column.

Neighborhood: The neighborhood of a home will be defined by a parameter R (this radius value will be an input to the model, so the value of R may vary from one simulation to another). The R-neighborhood of the home at Location $(i,j)$ contains all Locations $(k,l)$ such that:

$0 \le k \lt N$ and $i-R \le k \le i+R$
$0 \le l \lt N$ and $j-R \le l \le j+R$

Note that the Location $(i,j)$ itself is considered part of its own neighborhood. So, every homeowner will have at least one neighbor (himself).

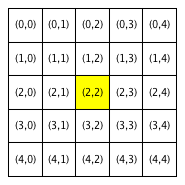
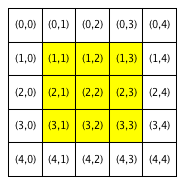
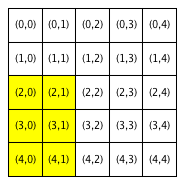
We will refer to a neighborhood with parameter R=x as an “R-x neighborhood”. The following figure shows the neighborhoods around Locations (2,2) and (3,0) for different values of R. Cells colored yellow are included in the specified neighborhood.

Neighborhood around (2,2)		Neighborhood around (3,0)
R = 0	R = 1	R = 1	R = 2

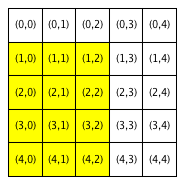Notice that Location (3,0), which is closer to the boundaries of the city, has fewer neighboring homes for the same value of R than Location (2,2), which is the middle of the city. We use the term boundary neighborhood to refer to a neighborhood that is near the boundary of the city and thus does not have a full set of neighbors.

Satisfaction: For each homeowner, we are going to compute a similarity score S/H where S is the number of homes in the neighborhood with occupants of the same color as the homeowner and H is the number of occupied homes in the neighborhood. Since a homeowner is included in his own neighborhood, S will always be at least one and H will be at least one. A homeowner is satisfied with her location, if her similarity score is greater than or equal to a specified threshold.

The figure below illustrates this concept using a city with R-1 neighborhoods. It shows homeowners and their similarity scores. White cells depict unoccupied homes/locations. Blue and red cells hold blue and red homeowners respectively. Each grid cell contains its location (in parentheses) and, for occupied homes, the homeowner’s R-1 similarity score (in square brackets). We rounded the similarity scores in the figure to three digits merely for clarity. Do not round them in your computation.

Similarity scores
R=1

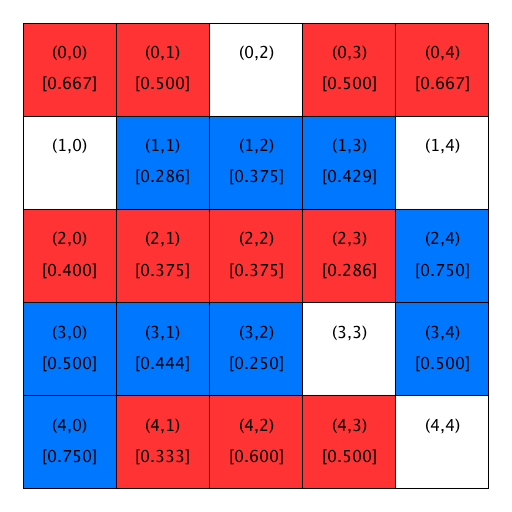The next two figures illustrate the effect of the threshold on satisfaction. The figure on the left was computed using a threshold of 0.33, while the figure on the right was computed using a threshold of 0.60. As in the figure above, white locations are unoccupied. In these figures, blue (red) locations are occupied by satisfied blue (red) homeowners, while light blue (pink) locations are occupied by unsatisfied blue (red) homeowners.

Satisfaction threshold = 0.33	Satisfaction threshold = 0.60
R=1	R=1

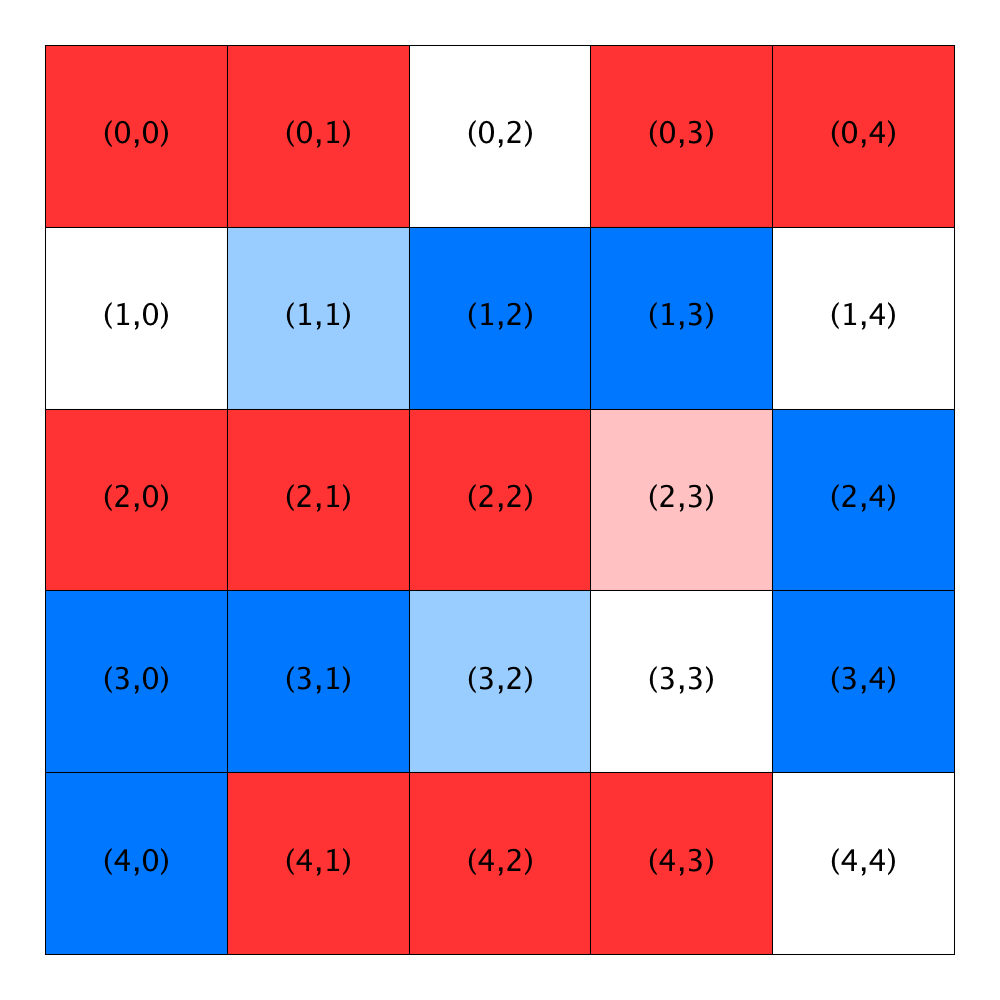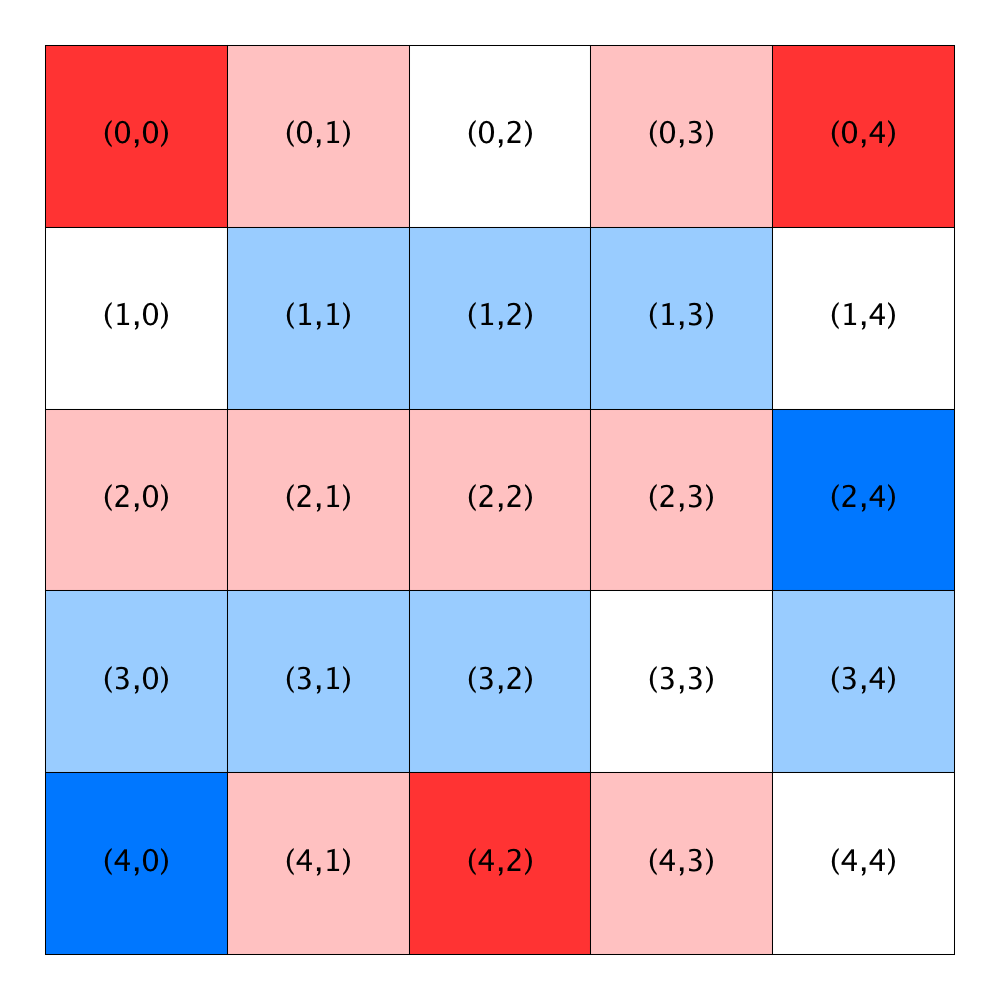The threshold is a parameter of the model, and will be the same for all the homeowners in a given simulation.

Relocation rule: If possible, an unsatisfied homeowner should be relocated to an open location that meets the satisfaction criteria. Our homeowners are picky: they want to move to satisfactory locations, but would prefer to stay in integrated neighborhoods. Also, they are looking for a good deal and so, prefer homes that have been on the market longer. To state these preferences more precisely: given multiple (unoccupied) homes that meet the satisfaction threshold, an unsatisfied homeowner will choose the home with the most diversity, that is, the lowest satisfaction score that is at or above the threshold. In case of ties, the homeowner will choose the home that has been on the market longest. If none of the available homes are satisfactory, then the homeowner will not relocate.

We will model the homes that are currently available with a list of their locations. Once a homeowner chooses a home, the location of his new home should be removed from the list and the location of his previous home should be added to the end of the list of available homes. That is, we will be keeping this list of homes in order from oldest listing to newest listing.

Here is an example relocation of the unsatisfied homeowner at Location (1,1) to Location (1, 4):

Before relocation	After relocation

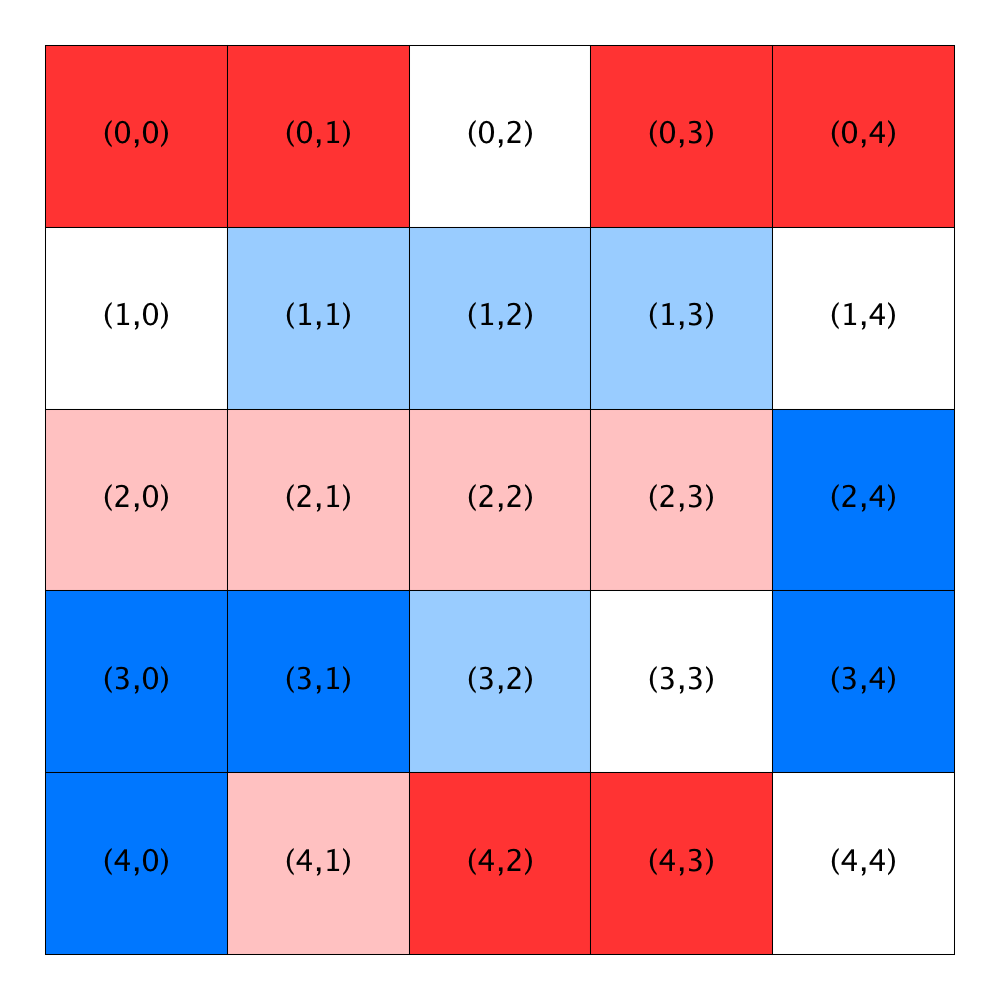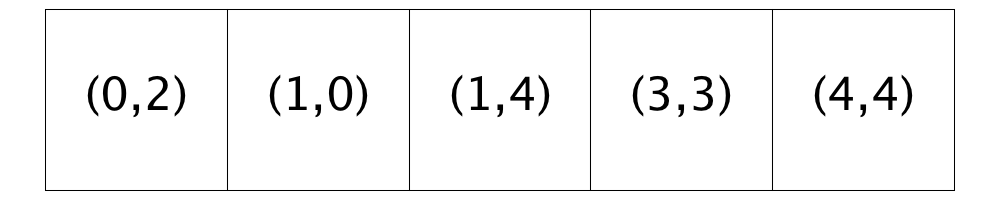
On the left, we show a city with R-1 neighborhoods with a satisfaction threshold of 0.44 along with a depiction of the locations that are open in the neighborhood (shown below the grid). The homeowner in Location (1,1) is unsatisfied with his location. He considers all five open locations and finds the following:

Location	Similarity Score	Satisfactory	Threshold Difference
Location (0, 2)	0.6	Yes	0.15999999999999998
Location (1, 0)	0.2	No
Location (1, 4)	0.5	Yes	0.06
Location (3, 3)	0.5	Yes	0.06
Location (4, 4)	0.6666666666666666	Yes	0.22666666666666663

All the open locations except Location (1, 0) have acceptable similarity scores. Locations (1, 4) and (3, 3) have the scores that are closest to the threshold. Of these, the homeowner will choose Location (1,4) because it is closer to the front of the list (that is, it came on the market sooner).

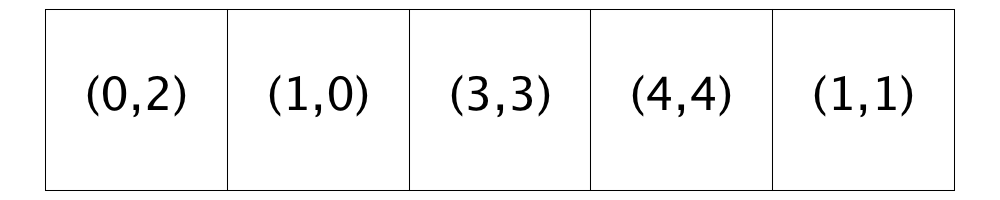
The frame on the right shows the state of the neighborhood after this homeowner has been relocated. Notice that Location (1,4) has been removed from the list of open locations and Location (1,1) has been added to the end of the list. Also, notice that the satisfaction states of the homeowners at Locations (0,3), (1,3), and (2,0) have changed. Can you figure out why?

Simulation Step: During a step in the simulation, your implementation should make a full pass over the city in row major order. As your implementation visits each home, you will check to see if the home is occupied and if so, whether the homeowner is satisfied with her location at the time of the visit. If she is satisfied, then you will move on to the next home in the traversal. If not, you should attempt to relocate her to a more satisfactory location using the relocation rules described above.

To recap: a visit to a particular home will trigger a relocation in a given step if, at the time of the visit:

the home is occupied;
the homeowner is unsatisfied with his location; and
there is an open location that meets the satisfaction criteria.

Stopping conditions: Your simulation should stop when:

it has executed a specified maximum number of steps or
no relocations occur in a step.

Sample simulation: step 1

In the figure below, the first frame represents the initial state of a city. The next five frames illustrate the relocations that occur in the first step of the simulation.

Step 1
Initial state	After 1st relocation	After 2nd relocation	After 3rd relocation


After 4th relocation	After 5th relocation

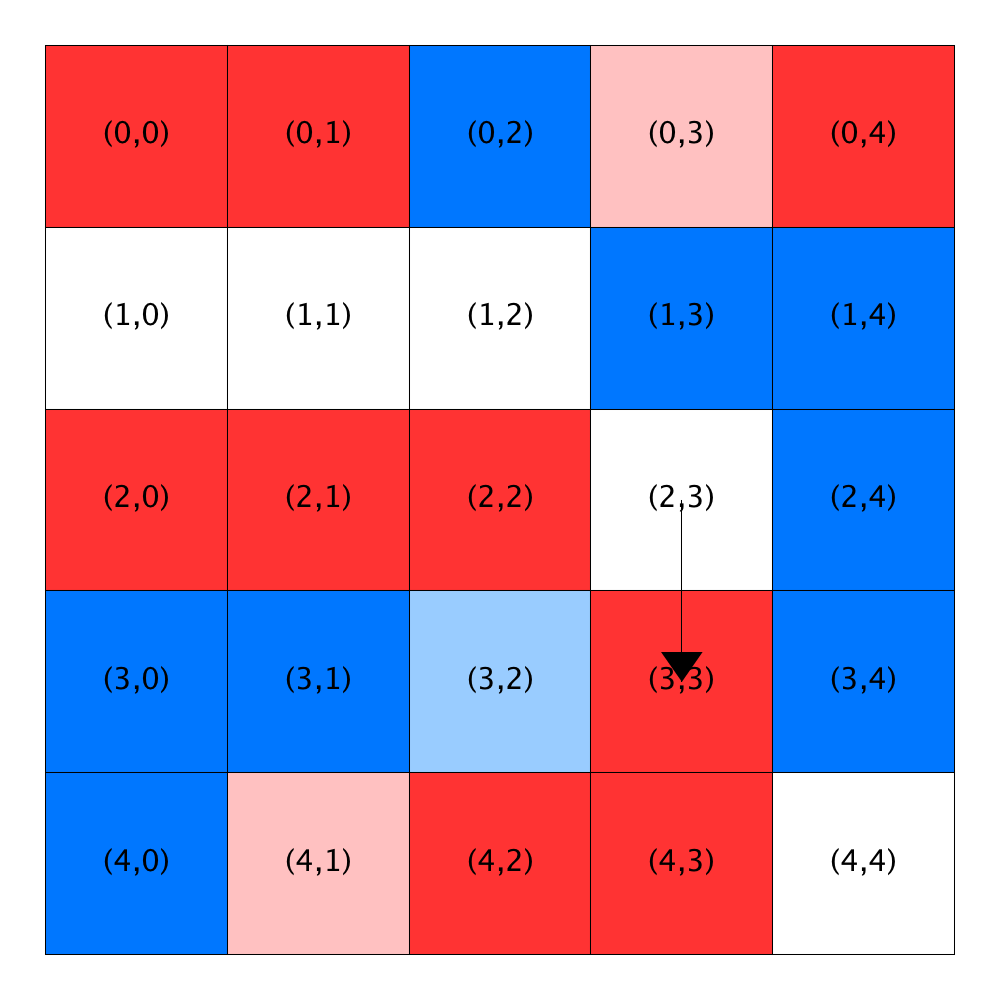
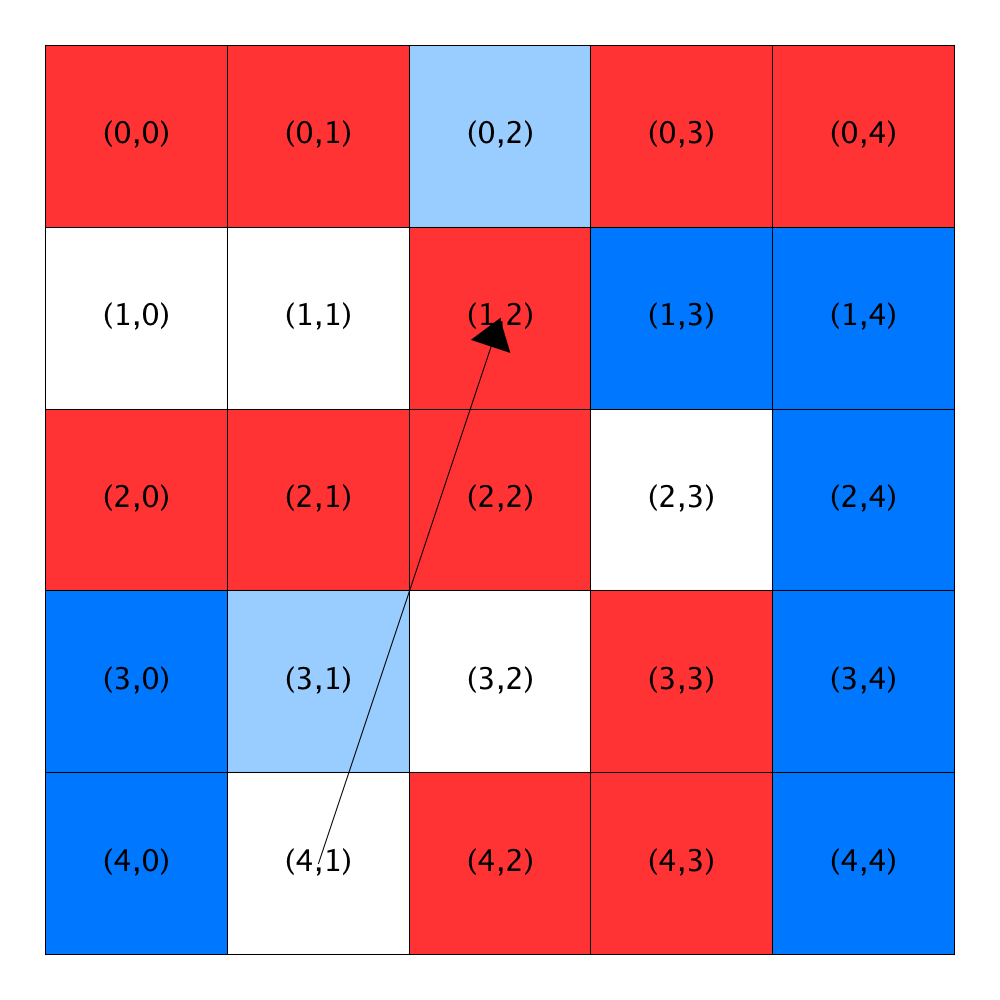
At the start of step 1, all of the homeowners in row 0 (that is, in Locations (0,0), (0,1), (0,3), and (0,4)) are satisfied. The homeowner in Location (1,1) is the first unsatisfied homeowner encountered during our traversal of the city. As discussed above in the relocation example, the homeowner will move to Location (1,4), because

the neighborhood around this location is satisfactory,
this home tied with one other home (at Location (3,3)) for the best similarity score, and
it has been on the market longer than the home at Location (3,3) (i.e., it appears earlier in the list of open homes).

Notice in the figure labelled “After 1st relocation” that Location (1, 4) has been removed from the list of open locations and Location (1,1) has been added to the end of the list.

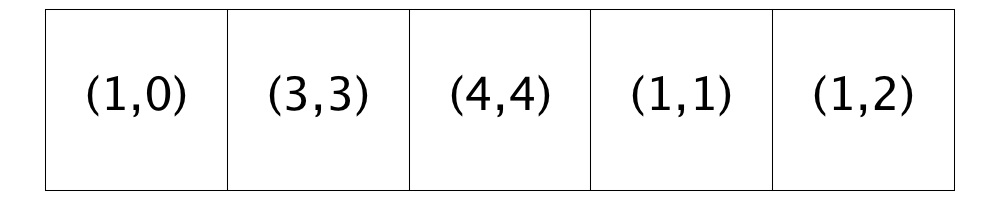
Relocating the blue homeowner at Location (1,1) causes the blue homeowner at Location (1,2) to become unsatisfied. And as it happens, this location is the next in our row-major traversal. Three of the five open homes (Locations (0,2), (3,3), and (4,4)) are suitable for the blue homeowner at (1,2). The homeowner will move to Location (0,2) because it ties with Location (3,3) for the best similarity score and it appears earlier in the list of open homes.

The traversal continues past satisfied homeowners in Location (1,3), Location (1,4), etc., until it reaches an unsatisfied red homeowner at Location (2,3). All five open homes are suitable for this homeowner, but Location (3,3) has the best similarity score. And so, the homeowner in Location (2,3) will move to Location (3,3).

The traversal then continues past satisfied homeowners at Locations (2,4), Location (3,0), etc., until it reaches the unsatisfied homeowner at Location (3,2). Again, all the currently open locations are satisfactory, but Location (4,4) has the best similarity score.

The next three spots in the traversal (Locations (3,3), (3,4) and (4,0) have satisfied homeowners. The fourth, the red homeowner at Location (4,1), is unsatisfied. Four of the five currently available homes are satisfactory (all but Location (2,3)) and of those, Location (1,2) has the best similarity score and so, the homeowner moves from Location (4,1) to Location (1,2).

The homeowners in the remaining locations in the traversal are all satisfied and so no further relocations occur in this step.

Sample simulation: step 2

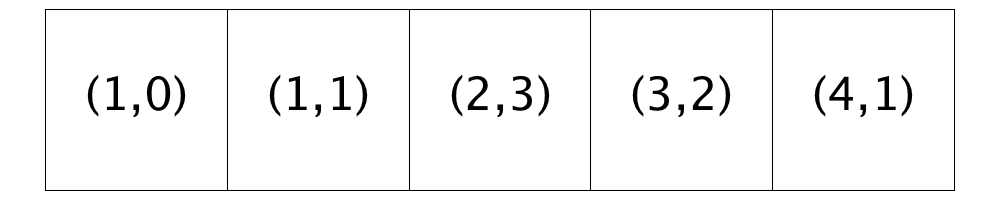
The first frame in the figure below represents the state of a city at the start of the second step. Notice that both the state of the grid and the open locations list are the same as they were at the end of the first step.

Step 2
Initial state	After 1st relocation	After 2nd relocation

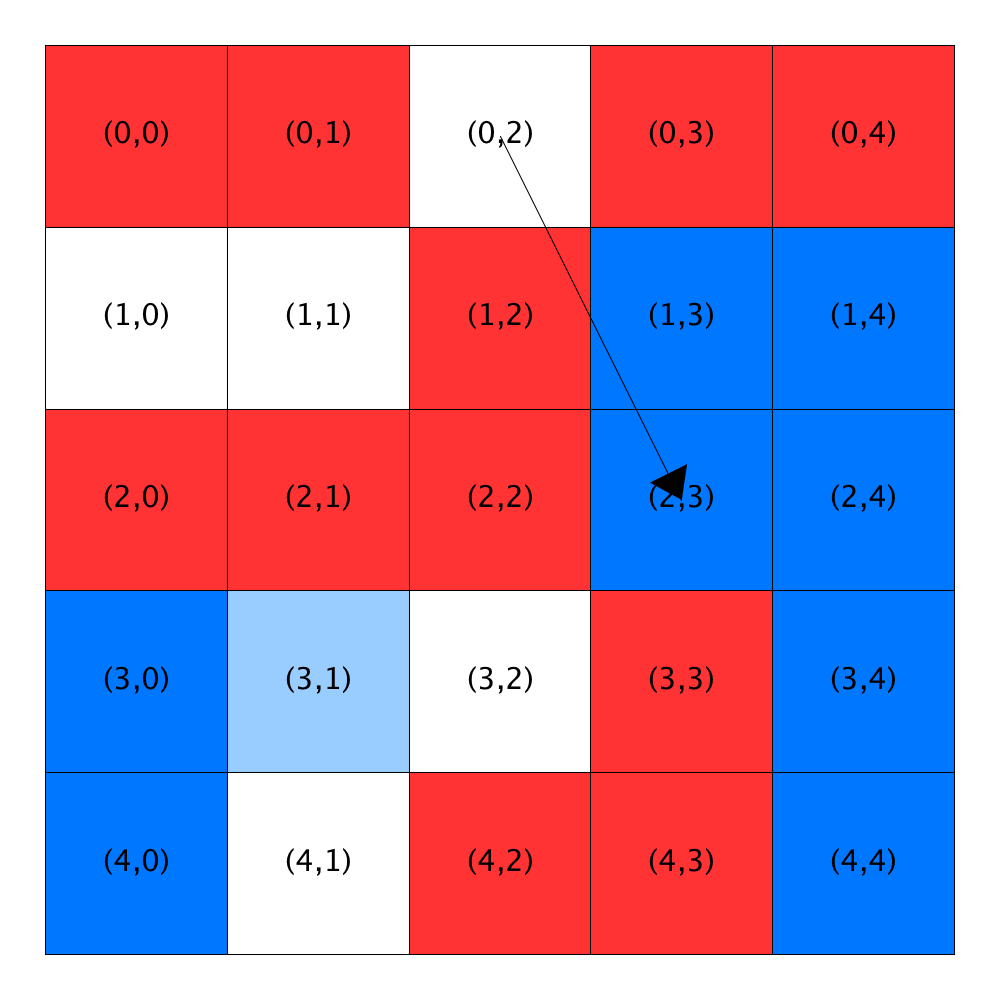
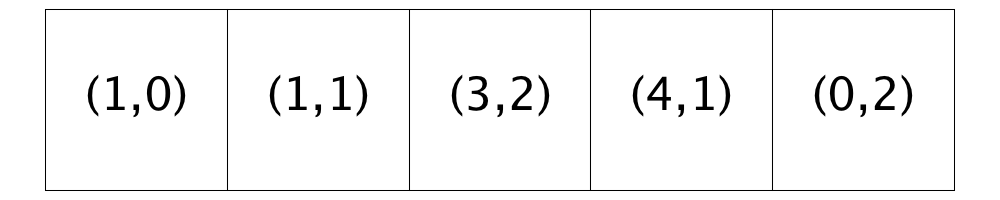
The traversal restarts at Location (0,0) and does not encounter an unsatisfied homeowner until Location (0,2). This homeowner is moved to Location (2,3), because it has the best similarity score of the two homes that are suitable (Locations (2,3) and (4,1)).

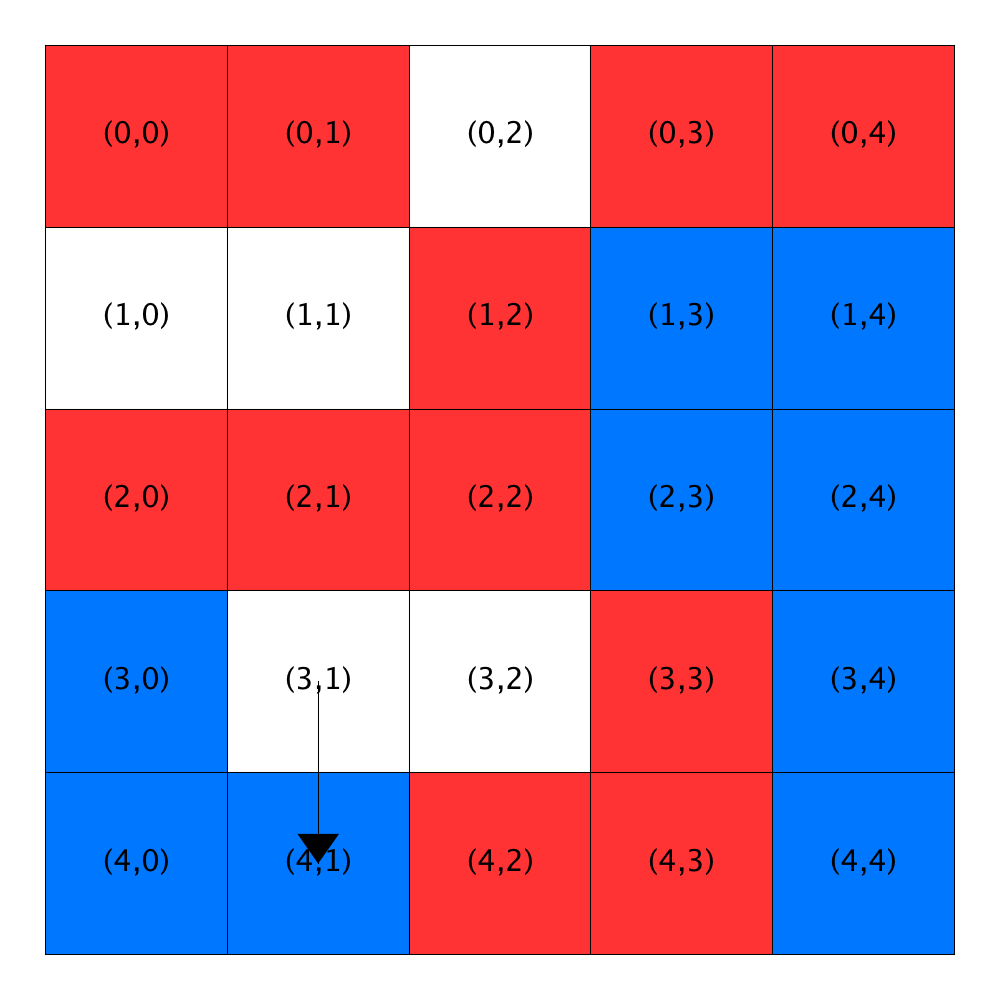
Next, the traversal passes 13 homes before it gets to an unsatisfied homeowner at Location (3,1). Only one currently available location (Location (4,1)) has an acceptable similarity score and so, the homeowner moves to it.

All the rest of the homes encountered during the traversal are either open or have satisfied homeowners, so no further relocations occur.

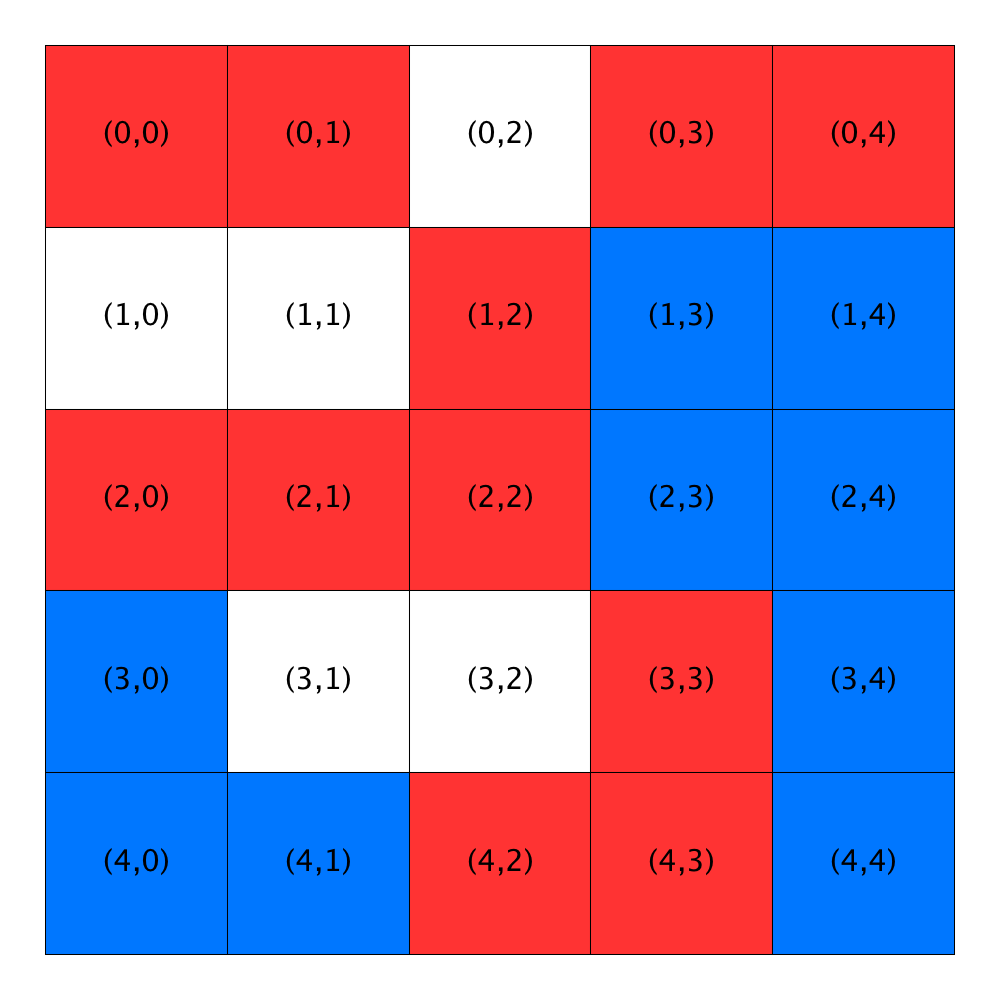
Sample simulation: step 3

The first frame in the figure below represents the state of a city at the start of the third step. At this point, all the homeowners are satisfied, so no relocations happen during the third step traversal and the simulation halts when the traversal is completed.

Step 4
Initial state	Final state

Data representation¶

Your implementation will need a representation for the current state of a homeowner, a representation for the city (aka the grid), and a representation for the locations that are currently open (unoccupied).

Representing Homeowners/Homes: Homeowners will be represented by the strings “B” and “R”, and open homes are represented by “O” (the letter).

Representing cities: We will represent a city using a list of lists with strings as elements. You can assume that these strings will always be one of “B”, “R”, or “O”. Traversals of the city should always be done in row-major order.

The directory pa2/tests contains text representations of some sample city grids, including all of the grids shown above (see tests/a17-sample-grid.txt). See the file tests/README.txt for descriptions of the grid file format and the grid files included in the tests sub-directory.

The file utility.py contains some functions that you might find using when testing your code:

read_grid: takes the name of a grid file as a string and returns a grid. Here is a sample use that assumes utility has been imported:
```
utility.read_grid("tests/a17-sample-grid.txt")
```
is_grid(grid): does grid have the right type and shape to be a city grid?
print_grid(grid): takes a grid and prints it to stdout.
find_mismatch(grid0, grid1): takes two grids and returns the first location at which they differ. This function returns None if the grids are the same.

Representing Locations: We will use pairs (tuples) of integers to represent locations.

Tracking open locations We will use a list of pairs (locations) to track open locations.

Your implementation should initialize the list of open locations in the grid exactly once at the start of a simulation, using a row-major ordering. All subsequent changes to the list will occur as the result of a relocation.

When looking for a new location for a homeowner, your implementation will walk through the list of open locations and consider them as possible new homes for the homeowner. If this process evaluating new homes for a homeowner determines that he should move to a new location, you should remove this location from the list (using del or remove) and append his old location to the end of the list (using append).

We encourage you to look carefully at the open locations list in the sample simulation above. In particular, notice that we do not recompute the list of open locations between steps.

Code structure¶

Your task is to implement a function:

def do_simulation(grid, R, threshold, max_steps)

that executes simulation steps on the specified grid until one of the stopping conditions is met. This function must return the number of relocations done during the simulation. Your function can and should modify the grid argument. At the end of the simulation, the grid should reflect the relocations that took place during the simulation.

When designing your function decomposition, keep in mind that you need to do the following subtasks:

compute a homeowner’s similarity score;
create and initialize the list of open locations;
swap the values at two locations;
evaluate the open locations as potential new homes for a homeowner;
simulate one step of the simulation;
run steps until one of the stopping conditions is met.

Do not combine the last three tasks into one mega-task, because the resulting code would be hard to read and debug. You will lose significant style points if you have a mega-task.

Testing¶

We strongly encourage you to test your functions as you write them! The surest way to guarantee that you will need to spend hours debugging is to write all your code and only then start testing.

We have provided some test code for you, but you will also need to design some tests of your own.

Testing by hand

Recall that you can set-up ipython3 to reload code automatically when it is modified by running the following commands after you fire up ipython3:

%load_ext autoreload
%autoreload 2

and then loading the code for the first time:

import schelling, utility

(Do NOT add the .py extension when you import schelling and utility. We believe that doing so may be the source of the mysterious problem that some students encountered in PA #1 that caused python code to be replaced with postscript.)

Once you have done these tasks, you can test your code by hand: simply read a grid from a file and then call the function with the appropriate arguments. For example, if you wanted do a few quick tests of your compute_similarity_score function, you could do something like the following:

grid = utility.read_grid("tests/a17-sample-grid.txt")
schelling.compute_similarity_score(grid, 0, (0, 0))   # expected result: 1.0
schelling.compute_similarity_score(grid, 1, (0, 0))   # expected result: 0.6666666666666666
schelling.compute_similarity_score(grid, 2, (0, 0))   # expected result: 0.7142857142857143

The function compute_similarity_score does not modify the grid and so, it is not necessary to reload the grid between tests. On the other hand, the grid does need to be reloaded when testing do_simulation:

grid = utility.read_grid("tests/a17-sample-grid.txt")
schelling.do_simulation(grid, 0, 0.44, 1)  # do one step

grid = utility.read_grid("tests/a17-sample-grid.txt")
schelling.do_simulation(grid, 0, 0.44, 3)  # do all three steps.

Testing similarity scores

To encourage you to separate out the task of computing a homeowner’s similarity score, we have provided test code for such a function. Our code assumes that you have written a function with the header:

def compute_similarity_score(grid, R, location)

that computes the similarity score of the homeowner at the specified location for neighborhood defined by R.

For each test case, our test code reads the input grid from a file, calls your compute_similarity_score function with the grid and the other parameters specified for the test case, and checks the actual result against the expected result. Here is a description of the tests:

Tests for `compute_similarity_score`¶
Test number	Grid filename	R	Location	Expected result	Purpose
0	tests/a17-sample-grid.txt	0	(0, 0)	1.000000	Check boundary neighborhood:top left corner.
1	tests/a17-sample-grid.txt	1	(0, 0)	0.666667	Check boundary neighborhood:top left corner.
2	tests/a17-sample-grid.txt	2	(0, 0)	0.714286	Check boundary neighborhood: top left corner.
3	tests/a17-sample-grid.txt	0	(0, 4)	1.000000	Check boundary neighborhood: top right corner.
4	tests/a17-sample-grid.txt	1	(0, 4)	0.666667	Check boundary neighborhood: top right corner.
5	tests/a17-sample-grid.txt	2	(0, 4)	0.571429	Check boundary neighborhood: top right corner.
6	tests/a17-sample-grid.txt	0	(4, 0)	1.000000	Check boundary neighborhood: lower left corner.
7	tests/a17-sample-grid.txt	1	(4, 0)	0.750000	Check boundary neighborhood: lower left corner.
8	tests/a17-sample-grid.txt	2	(4, 0)	0.444444	Check boundary neighborhood: lower left corner.
9	tests/a17-sample-grid.txt	0	(1, 1)	1.000000	Check interior R-0 neighborhood.
10	tests/a17-sample-grid.txt	1	(1, 1)	0.285714	Check neighborhood that is complete when R is 1.
11	tests/a17-sample-grid.txt	2	(1, 1)	0.461538	Check neighborhood that is not complete when R is 2.
12	tests/a17-sample-grid.txt	2	(2, 2)	0.550000	Check neighborhood that corresponds to the whole city.
13	tests/grid-no-neighbors.txt	1	(2, 2)	1.000000	Check interior neighborhood with location that has no other neighbors.
14	tests/grid-no-neighbors.txt	1	(4, 4)	1.000000	Check boundary neighborhood (lower right corner) with location that has no other neighbors.
15	tests/grid-no-neighbors.txt	2	(4, 4)	0.250000	Check boundary neighborhood (lower right corner) with location that has a few neighbors.

Please keep in mind that even though there are many corner cases for this function, your code does not need to be complex! Our function, excluding the header comment, is about 15 lines of code.

As in PA #1, we will be using py.test to test your code. You can run our compute_similarity_score tests from a Linux terminal window with the command:

$ py.test -xv test_compute_similarity_score.py

(As in PA #1: we will use $ to signal the Linux command-line prompt.)

Recall that the -x flag indicates that pytest should stop when a test fails. The -v flag indicates that pytest should run in verbose mode. And the -k flag allows you to reduce the set of tests that is run. For example, using -k test_0 will only run the first test.

Testing the full simulation

We have also provided test code for do_simulation. For each test case, our code reads in the input grid from a file, calls your do_simulation function, checks the actual state of the grid against the expected state of the grid, and checks the actual number of relocations returned by do_simulation against the expected number of relocations.

Here is a description of the tests:

Tests for `test_do_simulation`¶
Test number	Input grid filename	Expected grid filename	R	Threshold	Maximum number of steps	Expected numer of relocations	Purpose
0	tests/a17-sample-grid.txt	tests/a17-sample-grid-1-44-0-final.txt	1	0.44	0	0	Check stopping condition #1
1	tests/a17-sample-grid.txt	tests/a17-sample-grid-1-20-2-final.txt	1	0.20	2	0	Check stopping condition #2
2	tests/grid-several-sat-first.txt	tests/grid-several-sat-first-1-20-2-final.txt	1	0.20	2	1	Check choosing among locations with acceptable similarity score.
3	tests/grid-several-sat-middle.txt	tests/grid-several-sat-middle-1-20-2-final.txt	1	0.20	2	1	Check choosing among locations with acceptable similarity score.
4	tests/grid-ties.txt	tests/grid-ties-1-20-2-final.txt	1	0.20	2	1	Check choosing among locations with same similarity score.
5	tests/grid-sea-of-red.txt	tests/grid-sea-of-red-1-40-1-final.txt	1	0.40	1	0	Check case where there no suitable homes.
6	tests/grid-sea-of-red.txt	tests/grid-sea-of-red-1-20-1-final.txt	1	0.20	1	1	Check case where possible new location is in the homeowner’s current neighborhood
7	tests/grid-sea-of-red.txt	tests/grid-sea-of-red-1-30-1-final.txt	1	0.30	1	0	Check case where possible new location is in the homeowner’s current neighborhood
8	tests/a17-sample-grid.txt	tests/a17-sample-grid-1-44-1-final.txt	1	0.44	1	5	Check sample grid after 1 simulation step
9	tests/a17-sample-grid.txt	tests/a17-sample-grid-1-44-2-final.txt	1	0.44	2	7	Check sample grid after 2 simulation steps
10	tests/a17-sample-grid.txt	tests/a17-sample-grid-1-44-3-final.txt	1	0.44	3	7	Check sample grid after 3 simulation steps
11	tests/a17-sample-grid.txt	tests/a17-sample-grid-2-44-4-final.txt	2	0.44	4	0	Check stopping condition #2.
12	tests/a17-sample-grid.txt	tests/a17-sample-grid-2-44-7-final.txt	2	0.44	7	0	Check sample grid with R of 2
13	tests/large-grid.txt	tests/large-grid-2-33-20-final.txt	2	0.33	20	149	Large grid

You can run the following command from a Linux terminal window:

$ py.test -xv -k "not large" test_do_simulation.py

to run all the tests except the one that uses the large grid. We encourage you to run the large test only after you have successfully passed all the small tests!

Running your program¶

The go function is the “main function” supplied in schelling.py that parses the command-line arguments, reads a grid from a file, calls your do_simulation function, and if the grid is small, it prints the resulting grid.

The command line arguments are: the name of the input grid file, a value for R, a value for the satisfaction threshold, and a maximum number of steps. For example, running the following command from the Linux terminal window:

$ python3 schelling.py --grid_file=tests/a17-sample-grid.txt --r=1 --threshold=0.44 --max_steps=1

will do a simulation using the grid specified in the file tests/a17-sample-grid.txt, with R=1, a threshold of 0.44, and a maximum number of steps of 1.

Drawing a grid¶

We have provided some code to allow you to look at a pictorial representation of a grid similar to those shown in the assignment description. The figures show whether a home is empty, occupied by a red homeowner, or occupied by a blue homeowner. They do not include any indication of whether the homeowner is satisfied. To use this code, run the following command in a Linux terminal window:

$ ./drawgrid.sh <grid filename>

where <grid filename> is replaced with the name of a grid file. For example, to draw the grid in tests/a17-sample-grid.txt, you would run the command:

$ ./drawgrid.sh tests/a17-sample-grid.txt

This program will pop up a new window with the drawing. To exit, click on the red circle on the top-left part of the window.

Grading¶

Writing code that produces the correct answer is not sufficient. You must also write clean and well organized code. We encourage you to review the CS121 Style Guide before you start writing code and to think carefully about your function decomposition.

Getting started/Submission¶

See these start-up and submission instructions if you intend to work alone.

See these start-up and submission instructions if you intend to work in a pair.

Acknowledgments: This assignment was inspired by a discussion of Schelling’s Model of Segregation in Housing in the book Networks, Crowds, and Markets by Easley and Kleinberg.