Lab #6: Recursion

Introduction

The objective of this lab is to give you practice in writing and calling recursive functions.

Getting started

Open up a Linux terminal and navigate (cd) to your cmsc12100-aut-20-username directory (where username) is your CNetID. Run git pull upstream master to collect the lab materials and git pull to sync with your personal repository.

The directory lab6 contains two Python files: a recursion.py file, where you will write all your code, and a tree.py file that is needed by one of the exercises.

Quick review

Recursion is the concept of defining something in terms of itself. In other words, by breaking it into similar, but smaller or simpler pieces, where these smaller or simpler pieces are defined in the same way as the larger piece. Because of this, the definition “folds” or “wraps” in upon itself.

For example, consider the calculation of factorial. The factorial of an integer is the product of itself and each of the smaller integers, down to one. For instance:

\[7! = 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\]

We could write a loop to evaluate factorial:

def fact(n):
  '''
  Compute n!
  '''

  rv = 1
  for k in range(1, n + 1):
    rv = rv * k
  return rv

This is a non-recursive version of factorial. Rather, it uses iteration.

But, we could also observe that we can break the calculation of factorial into a smaller case and then extend the result of the smaller case to the bigger one. In particular:

\[ \begin{align}\begin{aligned}7! &= 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\\7! &= 7 \cdot (6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1)\\7! &= 7 \cdot (6!)\\n! &= n \cdot (n-1) \cdot (n-2) \cdot ... \cdot 1\\n! &= n \cdot ((n-1)!)\end{aligned}\end{align} \]

This approach allows us to write a recursive version, a version where the function calls itself:

def fact(n):
  if n == 1:
    return 1
  return n * fact(n-1)

The last line is said to be the recursive case: the case where we call the same function again, but with a smaller input. The first case, the case where we are calculating the factorial of the number one, is called the base case, analogously to the base case in a proof by induction. This case is an exception to the general rule modeled by the recursive case. We do not want to calculate the factorial of one by referring to the factorial of a smaller number and possibly continuing the recursion down into the negative numbers. Instead, we want to define the value for this input as a hard-coded value with no further function calls.

Base cases are essential in recursion. They keep a recursive function from calling itself over and over again indefinitely. If a base case is missing, not only do we not get the correct answer, but we likely get no answer at all as the program attempts to recurse infinitely. When a recursive programs crashes or fails to complete a calculation, a missing base case is the likely culprit.

Part 1: Powers of two

If I give you a number, how can you tell if it is a power of two? (For this problem, we’re only going to consider non-negative, integer powers of two: 1, 2, 4, 8, …. We’re not talking about fractions, such as 1/2 or 1/4, or exponents that aren’t whole numbers.)

Here is a reasonable approach you might take: First, you might “eyeball” the number to see if you recognize it as a power of two; you have probably memorized many of the smaller such numbers over the years. Also, you might look for obvious clues that it is not a power of two (for instance, it is odd, and not one).

If those tactics did not yield an immediate answer, you might next refer to a logarithm table, or use a calculator to take a log. But suppose you don’t have these aids handy, or do not wish to pursue that approach.

You would then, probably, adopt a pencil-and-paper approach to determine if it was a power of two. This approach involves repeated calculations until you find evidence that the number is, or isn’t, a power of two.

Think about what those calculations would be, and how you can transform the question about a given number to one about a smaller number. (Hint: try to come up with an equation similar to the one we had for factorial.)

Task 1: Complete the function, is_power_of_two(n) in recursion.py.

In implementing this function, you may not use loops. While some problems, including this one, have iterative and recursive solutions that are both reasonble, the purpose of this problem is to practice recursion.

Part 2: Fibonacci

We’ll next write a slightly more complex recursive function.

The Fibonacci sequence begins as follows:

1, 1, 2, 3, 5, 8, 13, 21, 34, ....

The first two terms in the sequence are 1. Each subsequent term is the sum of the previous two. For example, sicne term 6 is 13 and term 7 is 21, we can calculate that term 8 is 13 + 21 = 34.

The Fibonacci sequence may be mathematically defined as follows:

\[\begin{split}F_0 &= 1 \\ F_1 &= 1 \\ F_n &= F_{n-1} + F_{n-2}\end{split}\]

Task 2: Complete the function:

def fib(n):

That takes an integer n as its input and returns the nth Fibonacci number. The above mathematical definition of Fibonacci numbers can be expressed in terms of evaluations of this function:

In [2]: fib(0)
Out[2]: 1

In [3]: fib(1)
Out[3]: 1

In [4]: n = 7  # you can set n > 1, and the result should not change

In [5]: fib(n) == fib(n-1) + fib(n-2)
Out[5]: True

What is different about this function in relation to the other recursive functions we’ve seen? Roughly how many steps does this implementation of Fibonacci take to complete? Can you think of an aspect of how this function is implemented that is particularly inefficient?

Think about how many times the function fib(3) will be called in the evaluation of fib(5).

It will be called by fib(5) for the \(n - 2\) case, but it will also be called by fib(4) in the \(n - 1\) case.

Both of the times it is called, it calculates the result from scratch.

The function fib is the kind of function that should be expected to have the same output for the same input. But for both of the times fib(3) is called, it must be computed again. This problem is magnified as the value of n increases.

This type of function — one which always has the same result for the same input — is called pure. If a function is known to be pure, you can be more clever by storing its result in memory the first time it is calculated, and then referring to the cached result if it is needed in the future rather than recalculating it. If you take further computer science courses, you will explore this concept more extensively.

Part 3: Finding roots

You may have encountered Newton’s Method in a math class; it is an approach to finding the roots of a function (places where the function is zero, or more precisely, \(x\)-values for which \(f(x) = 0\)). If this calculation does not sound extraordinarily useful in a wide variety of cases, keep in mind that you can rephrase the question “for what \(x\) is \(f(x) = y\)” into the question “for what \(x\) is \(f(x) - y = 0\)” by subtracting \(y\) from both sides of the equation, and then use Newton’s Method on the function \(g(x)\) where \(g(x)=f(x)-y\).

Here are a couple things you can do with this kind of algorithm:

  • Compute the square root (cube root, or any root) of a number. The square root of \(7\), for instance, is a root of the function \(f(x) = x^2 - 7\)

  • Compute inverse trigonometric functions. A root of \(f(x) = \sin(x) - 0.5\) is an angle \(x\) for which \(\sin(x) = 0.5\); this value is denoted by \(x = \sin^{-1}(0.5)\).

One practical issue with Newton’s Method is that it uses the derivative of the function. We may not have an equation for the derivative, so we may prefer to use one of the variants of Newton’s Method that is simpler. These variants include (in order of complexity) the Bisection Method, the Secant Method, and the False Position Method.

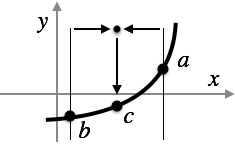
../../_images/bisection1.png

We will describe the Bisection Method for finding a root of a function. The Bisection Method begins with two \(x\)-values, \(a\) and \(b\), on either side of the root. In other words, \(f(a)\) and \(f(b)\) must have opposite signs. If the function \(f\) is continuous, then by the Intermediate Value Theorem, there must be an \(x\)-value between \(a\) and \(b\) such that \(f(x) = 0\). Put simply, the function has to pass through \(y = 0\) on its way between the negative \(y\)-value and the positive \(y\)-value.

However, we do not know where, between \(x = a\) and \(x = b\), this root might lie. But the Bisection Method simply tries the point \(x = c\), in the middle of \(a\) and \(b\), next.

There are a couple of possibilities at this point. First, \(c\) might actually be the root, or so close to it that we consider it close enough. In this case, we are done, and we call \(c\) the root. More likely, however, \(c\) is not close enough to the root. But, in that case, \(c\) is either positive or negative.

Think about how the problem of finding a root, now that we have evaluated \(f(c)\), has become a similar problem to the original problem of finding a root between \(a\) and \(b\). And why is this problem similar, but smaller/simpler?

What is the base case?

Ideally, our base case would be that \(f(c) = 0\). However, floating point calculations do not have perfect precision, and having a result that is exactly zero, with no error at all, is uncommon.

Thus, it is typical to use an “epsilon” value to specify what counts as “close enough” to zero. If you are not familiar with the practice, the Greek letter \(\varepsilon\) (epsilon) is commonly used refer to a very small, but non-zero, value. For instance, we might set \(\varepsilon = 0.001\) and accept any \(x\) for which \(-0.001 < f(x) < 0.001\).

So, we might choose to stop the recursion when we find a \(c\) such that the absolute value of \(f(c)\) is less than a specified \(\varepsilon\).

An alternative approach is to stop when the difference between \(a\) and \(b\) becomes small. However, we will use the condition involving \(f(c)\) and \(\varepsilon\) instead.

Task 3: Complete the function find_root_sqrt2 in recursion.py:

def find_root_sqrt2(epsilon, a, b):

that, for the function mentioned above that has a root at the square root of two, returns the a root, or rather, an \(x\)-value for which \(f(x)\) is within epsilon of zero. Place your implementation in recursion.py.

Then, test your find_root_sqrt2 function with epsilon values of 1, 0.1, 0.01, and 0.001. Use a = 0.0 and b = 2.0 as starting points,

Here are some hints for debugging:

  • You may want to print out the values of a, b, and c each time the function is called.

  • You should be able to, using pencil and paper, apply the Bisection Method yourself. The values of \(a\), \(b\), and \(c\) for each step that you come up with should exactly match what your code is doing. If they do not, try to understand the source of the discrepancy.

  • If your code always stops immediately in the base case without making even a single recursive call, modify your code to print out the value of c and epsilon and think about the test you are using to determine if c matches the base case. You might have forgotten something.

Part 4: Trees

Recursive functions are often used with recursively-defined data structures. In this part, you will work with a recursively-defined tree. We will use the same tree module you will be using in the programming assignment.

The code in recursion.py defines two trees, t0 and t1:

In [1]: t0.print()

node0: 27

In [2]: t1.print()

node0: 1
  │
  ├──node1: 2
  │  │
  │  └──node2: 3
  │
  ├──node3: 4
  │
  └──node4: 5

How would we define a function to compute the number of leaves (nodes with no children) in a tree? What is the base case? What are the recursive cases and how do we combine the results?

The recursion should stop when we hit a leaf, that is, when the input node has no children. If a node is not a leaf, then we need to compute the sum of the number of leaves in each of its children. Here is a straightforward translation of these requirements:

def count_leaves(t):
    '''
    Count the number of leaves in the tree rooted at t

    Inputs: (Tree) a tree

    Returns: (integer) number of leaves in t
    '''

    assert t is not None

    if t.num_children() == 0:
        return 1

    num_leaves = 0
    for kid in t.children:
        num_leaves += count_leaves(kid)

    return num_leaves

This function would return 1 when called with t0 and 3 when called with t1.

Task 5: Complete the function:

def add_values(t):

which should take a tree node and return the sum of the values in the tree rooted at that node. A call to add_values(t0) should return 27 and a call to add_values(t1) should return 15.

Our implementation of this function is very similar to the previous function.

When Finished

When finished with the lab please check in your work (assuming you are inside the lab directory):

git add recursion.py
git commit -m "Finished with recursion lab"
git push

Again, we’re not grading your work. We just want to make sure your repository is in a clean state and that your work is saved to your repository (and to our Git server).