cs223
Crash Course in Asymptotic Analysis
Let us review the basic mathematical techniques for describing the time- and space-efficiency of algorithms. First, we'll consider how to define the "costs" of algorithmic operations as functions of their inputs. Then, we'll consider tools for "comparing" these functions.
Recurrence Relations
Lookup in Lists
Here is a simple find (or "member") function that traverses the list xs:
find : a -> List a -> Bool
find x xs =
case xs of
[] ->
False
y::rest ->
if x == y then True else find x restWe want to define a function T(n) to describe the time cost of find, where n is the size of (i.e. number of elements in) the xs list.
There are three cases to consider:
If
xsis[], thenfindreturns after some constant c1 amount of work for the pattern matching. So, T(n) = c1.If the head
yof the list equalsx, thenfindreturns after some constant c2 amount of work for the pattern matching and equality test (note that we are assuming that(==)is a constant-time operation, which may not always be a reasonable assumption). So, T(n) = c2.Otherwise,
findperforms some constant c3 amount of work for the pattern matching and comparison and also recursively callsfindwith therestof the list. So, T(n) = c3 + T(n-1).
To compute an upper bound on the running time of find, we must consider the worst case, which means traversing the entire list without finding the desired element x. By unrolling the three cases above for the entire list, we obtain the following recurrence relation below:
T(n) = c3 + T(n-1)
T(n-1) = c3 + T(n-2)
T(n-2) = c3 + T(n-3)
...
T(1) = c3 + T(0)
T(0) = c1To compute a closed form solution for T(n), we sum the system of equations and obtain:
T(n) = n*c3 + c1Lookup in Sorted Lists
What about the running time of find if the input list xs is sorted? Even so, the worst case for the function is that x is absent from the list, and the only way to be sure is to traverse all of its elements.
Note that this linear search algorithm is guided by the constraint that, in a purely functional language, only the head of a list can be accessed at once. In a language with pointers or references, arbitrary elements of a list can be accessed in constant-time (such lists are usually called arrays). The cost of the binary search algorithm on sorted arrays has a much smaller asymptotic growth rate. (Later, we will see how purely functional languages typically provide an array data structure.)
Frivolous Version
frivolousFind x xs =
case xs of
[] ->
False
y::rest ->
let _ = length xs in
if x == y then True else frivolousFind x xsWhat's the running time of frivolousFind? How does it compare to find?
Big-O Notation
f(n) is O(g(n)) — read "f(n) is Big-O of g(n)" — if ∃ c > 0, N > 0 such that ∀ n ≥ N, f(n) ≤ c·g(n). Definitions sometimes vary in their uses of >, ≥, <, and ≤, but these differences do not matter much.

This notion says that, in the grand scheme of things, the particular constant factors don't matter. What matters is the shape of the curve seen from afar, in the limit. For example, maybe one curve dwarfs the other:

Or maybe they are indistinguishable:
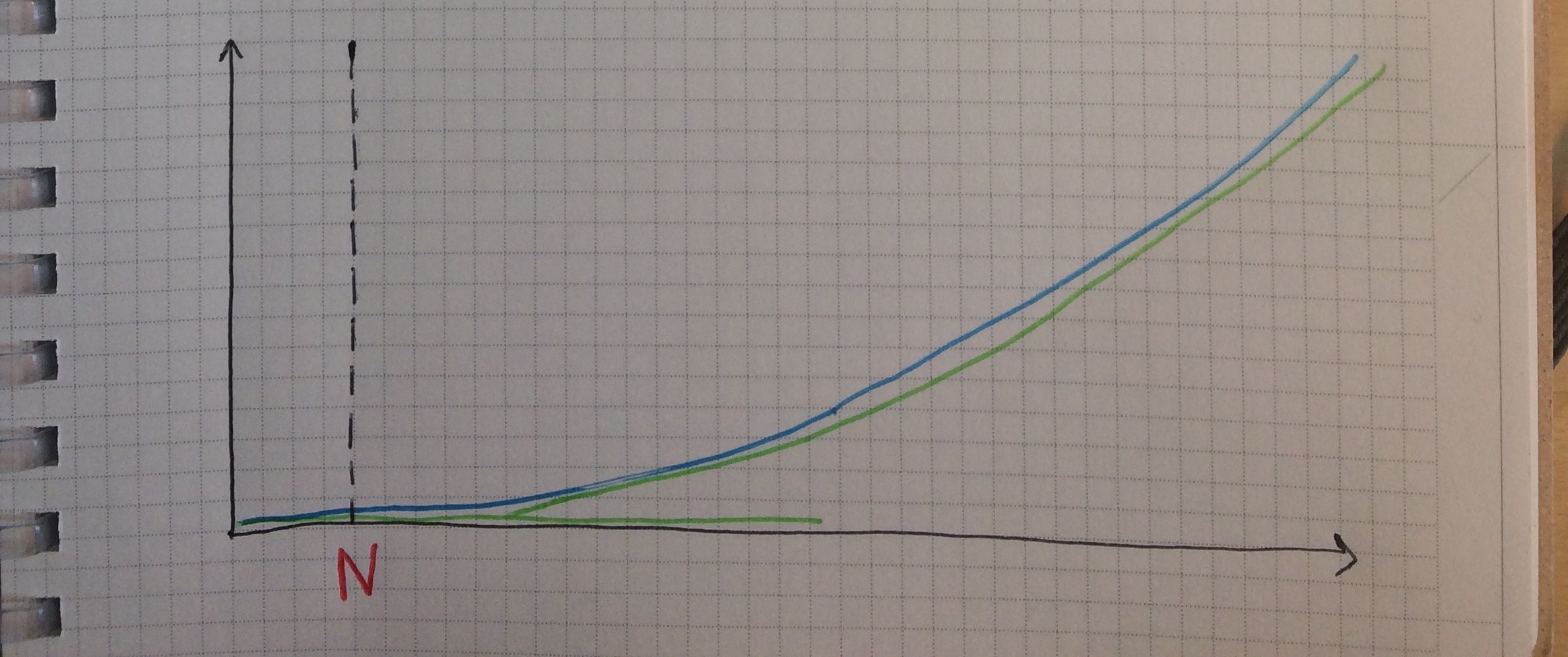
(This kind of reasoning is extremely useful. But in practice, compiler writers, library writers, and other programmers will sometimes need to pay meticulous attention to the constant factors exhibited by their algorithms.)
Example
- f1(n) = n/100
- f2(n) = 100n
- f3(n) = 100n + 23
f1(n) is O(n) because
- f1(n) ≤ n for all n ≥ 0.
f2(n) is O(n) because
- f2(n) ≤ 100·n for all n ≥ 0.
f3(n) is O(n) because
- f3(n) ≤ 101·n for all n ≥ 23, or
- f3(n) ≤ 102·n for all n ≥ 12, or
- f3(n) ≤ 111·n for all n ≥ 3, or
- f3(n) ≤ 200·n for all n ≥ 1, or ...
Terminology
In computer science settings, g(n) is often referred to as Big-Omega of f(n) — written g(n) is Ω(f(n)) — if f(n) is O(g(n)). However, this definition conflicts with other definitions of Big-Omega.
Tight Bounds
A Big-O relationship specifies an asymptotic upper bound but provides no information about how "tight" the bound is. For example, n2 is O(n4), but this bound is not as informative as other valid upper bounds.
It is often useful to establish a lower bound L(n) for a function f(n) (such that L(n) is O(f(n))) in addition to an upper bound U(n) (such that f(n) is O(U(n))). When L = U, the bound is referred to as tight.
Tight bounds are described by Big-Theta notation. That is, f(n) is Θ(g(n)) if f(n) is O(g(n)) and g(n) is O(f(n)).
Optional Exercise — Prove that for all i and j, logi(n) is O(logj(n)). Hint: for all b, logb(x) = (ln x) / (ln b).
Unless otherwise noted, we write O(log(n)) as shorthand for O(log2(n)). Considering the fact above, this convention is justified with respect to asymptotic growth rates.
Optional Exercise — Define an ordering [f1, f2, f3,...] of the functions below such that for all i and j, i < j implies fi is O(fj).
- 2n
- n
- 4
- sqrt(n)
- n2+3n
- log(n)
- n·log(n)
- n!
- n5 - n4
- 1.5n
Recurrence Relations (Continued)
We will consider a couple more simple algorithms that traverse data structures looking for a particular element.
Lookup in Lists (Redux)
T(n) = n*c3 + c1Because, T(n) is O(n), we say that find runs in worst-case O(n) time.
Lookup in Binary Trees
An analogous lookup function on binary trees:
type Tree a
= Empty
| Node a (Tree a) (Tree a)
findBT x t =
case t of
Empty ->
False
Node y left right ->
x == y || findBT x left || findBT x rightWithout knowing anything about the structure of the tree, findBT must search the entire tree, by recursively traversing the left and right subtrees in the worst case. What are the costs T(???) + T(???) of the two recursive calls? If the size of t = Node y left right is n, then the combined size of left and right is n-1. Therefore, making both recursive calls takes time T(n-1) in total. This leads to the following recurrence relation, where we make use of constants c and c' for operations involved in the worst (requiring both recursive calls) and best (inspecting the Empty tree) cases, respectively.
T(n) = c + T(n-1)
T(n-1) = c + T(n-2)
T(n-2) = c + T(n-3)
...
T(1) = c + T(0)
T(0) = c'
-------------------
T(n) = n*c + c'As a result, findBT runs in worst-case O(n) time.
Lookup in Binary Search Trees
A binary tree satisfies the binary search order property if for every subtree of the form Node x left right, all Nodes in left store values y such that y < x and all Nodes in right store values y such that x < y.
Assuming that t satisfies this ordering property, findBST is defined to look only in the subtree that contains the desired element x:
findBST x t =
case t of
Empty ->
False
Node y left right ->
if x == y then
True
else if x < y then
findBST x left
else {- x > y -}
findBST x rightThe recurrence relation for findBST, however, looks just like the one for findBT; even though only one recursive call is made in the worst case (either to left or right), the worst case size of the traversed subtree is n-1. Therefore, findBST runs in O(n) time.
Lookup in Balanced Binary Search Trees
If a binary-search ordered tree is also balanced, where every subtree's children are roughly the same size (there are various reasonable definitions, as we will see later in the course), then the recurrence relation for findBST is:
T(n) = c + T(n/2)
T(n/2) = c + T(n/4)
T(n/4) = c + T(n/8)
...
T(1) = c + T(0)
T(0) = c'
-----------------------
T(n) = (log n)*c + c'As opposed to n recursive calls in the worst case before, there are now at most log2(n) recursive calls, because each child tree is (roughly) half the size. Therefore, findBST runs in worst-case O(log2(n)) time when the tree is balanced.
Notice that we are not being thorough in tracking exactly what the sizes of subtrees are, and we are simply taking them to be half the size of the entire tree. Although this can be rigorously worked out, in the end it does not matter, because of the wiggle room provided by the constants and inequalities in the definitions of rates of growth. If you are not already comfortable with this material, you may wish to read more background on these topics.
Space
The examples above considered time costs. What about space costs?
- "Heap space" is memory dedicated to the data created during evaluation.
- "Stack space" is memory dedicated to managing any outstanding function calls during evaluation.
We'll consider these next, in Persistence and Tail Recursion.
Reading
Optional
- A comprehensive presentation of these topics can be found in the classic CLRS textbook.