Goals for this homework

  • Practice with object-oriented concepts - inheritance and polymorphism
  • Transitioning to matrix-multiplication operations
  • Combining and splitting qubits mathematically
  • Providing full functionality for all gates - accepting any superposition state and properly calculating the results.

You are expected to complete this assignment individually. If you need help, you are invited to come to office hours and/or ask questions on Canvas. Clarification questions about the assignments may be asked publicly. Once you have specific bugs related to your code, make the posts private.

In this lab, we are adding the functionality to perform arbitrary operations on multiple qubits using matrix multiplication. In addition, we need to be able to combine a two single qubits into a two-qubit entity.

We would like to have some consistency between how we treat qubits, regardless of the width. The way we'll do this is practice with the concrete one- and two-qubit cases, then create a n-qubit class. All three of these classes will have distinct similarities, which we will define in a general Qubit class from which they will all inherit. This week, we'll do the one- and two-qubit options. Next week, we'll generalize to n-qubit.

If you want to add "helper" functions that aren't specified in the assignment, you are welcome to do so. If you want it to be used by all classes, place it in the parent class. If it is specific to a subclass, place it there. We will only test the functions specified, but you're always allowed to add private or protected methods.

You should submit several files for this assignment ( ParentQubit.java SingleQubit.java, DoubleQubit.java, TestQubits.java and Makefile) in your subversion repository as directed below.

This continues to refine and advance your quantum simulator. You began by viewing qubits like the visual representation, and you will need to make a transition to the mathematical representation. While it is possible in this lab to mostly stay with the original representation, there are a few methods that are very difficult to implement that way. So I would suggest making the transition to the vector / matrix representation now if you can. You definitely will need to next week, so you might as well now.

Set Up

Make sure you add to your Makefile as you complete classes.

Now you need to make the skeleton code so that your program will minimally execute. You must do this in case you do not complete your assignment. Our testing infrastructure needs to compile and execute even if you did not complete the entire assignment.

  • Step 1: Create all of the .java files. Each class requires its own file, named classname.java. For each method, implement the method with a single line - return with the right type. For example: 
    public class Blah {
  public double surface_area_cylinder(double height, double radius)
  {
	return 0.0;
  }
}
  • Step 2: Create TestQubits.java. For each method, put in a single method call. This single test file will end up testing all of your new classes. Most of the classes are so small they don't merit their own test file. For example: 
    public static void main(String[] args)
{
	Blah b = new Blah();
	b.surface_area_cylinder(1.0, 5.0);
	// add the rest of the method calls here
}
First get this compiling and running. It won't print out anything, but this will mean that your code will compile and execute with our infrastructure. This must work in order to get any points in this course. Do this first, not last.

Step 1: ParentQubit class

The ParentQubit class is an abstract class. That means we will never have an instance of ParentQubit itself, only of a subclass of it - its purpose is to provide some functionality but also define other functionality that is required to be implemented in subclasses (SingleQubit, DoubleQubit, and, later, NQubit). You need to decide the data that ParentQubit will contain for the state.
  • public ParentQubit(int numqubits);
    // Constructor: initialize all bits to 0
  • public void setValue(float v, int i);
    // The value in v is the probability of the ith value measuring that combination.
    // Combinations are always ordered in increasing order from 0 to (2^numqubits)-1.
    // Values are negative if the phase should be negative.
  • public void setValues(float[] v);
    // v is the length equal to the number of qubit combinations (2^numqubits).
    // The value in v[i] is the probability of measuring that combination.
    // Combinations are always ordered in increasing order from 0 to (2^numqubits)-1.
    // Values are negative if the phase should be negative.
  • public float getValue(int i);
    public float[] getValues();
  • public void setPhase(int p, int i);
    public void setPhases(int[] p);
    // these are analogous to the description above, but only for phase
    public int getPhase(int i);
  • public int getNumQubits(); // this returns the number of qubits this object represents
  • abstract ParentQubit mergeQubits(ParentQubit pq);
    // this merges two sets of qubits and returns a new one that has
    // a number of qubits that is the sum of the two. For example, we could
    // merge two SingleQubit objects to become one DoubleQubit object.
    // this is not implemented in ParentQubit but in the subclasses
  • abstract String toBraKet();
    // this prints out the state in bra-ket notation, like last week
  • abstract void applyNotGate();
    // apply a not gate to each qubit
  • abstract void applyNotGate(int qb);
    // apply a not gate to the qubit in position qb, where numbering starts at 0
  • abstract void applyHGate();
    // apply an H gate to each qubit
  • abstract void applyHGate(int qb);
    // apply an H gate to the qubit in position qb, where numbering starts at 0
  • abstract void applySwapGate(int qubit1, int qubit2);
    // apply a swap gate between qubit1 and qubit2, where numbering starts at 0

Step 2: SingleQubit

The next step is to implement your first subclass. You will begin with SingleQubit, which you already implemented in a slightly different way. Now you'll need to implement it in a way that is more consistent with generalizing to multiple qubits.
  • public SingleQubit();
    // Constructor: initialize bit to 0
  • ParentQubit mergeQubits(ParentQubit pq);
    // this merges two sets of qubits and returns a new one that has
    // a number of qubits that is the sum of the two. You are implementing
    // merging a SingleQubit with another SingleQubit. You will need to verify
    // that the input only has one Qubit. If it has more than one qubit, then
    // return null. Otherwise, create a DoubleQubit object and fill it in
    // with the proper values.
  • public String toBraKet();
    // this prints out the state in bra-ket notation, like last week
  • public void applyNotGate();
    // apply a not gate to the qubit
  • public void applyNotGate(int qb);
    // apply a not gate to the qubit in position qb, where numbering starts at 0
    // only do so if qb = 0
  • public void applyHGate();
    // apply an H gate to each qubit
  • public void applyHGate(int qb);
    // apply an H gate to the qubit in position qb, where numbering starts at 0
    // only do so if qb = 0
  • public void applySwapGate(int qubit1, int qubit2);
    // do nothing

Step 3: DoubleQubit

The next step is to implement DoubleQubit. Now you will implement this methods when you ahve two qubits.

  • public DoubleQubit();
    // Constructor: initialize bit to 0
  • ParentQubit mergeQubits(ParentQubit pq);
    // this merges two sets of qubits and returns a new one that has
    // a number of qubits that is the sum of the two. Next week, you will
    // merge a DoubleQubit to something of any size and create an NQubit.
    // This week, you merely return null.
  • public String toBraKet();
    // this prints out the state in bra-ket notation, like last week
  • public void applyNotGate();
    // apply a not gate to all qubits
  • public void applyNotGate(int qb);
    // apply a not gate to the qubit in position qb, where numbering starts at 0
    // only do so if qb = 0 or 1
    // derive the matrix by writing out the start and end states and mapping back to matrix.
    // this video goes over this process.
  • public void applyHGate();
    // apply an H gate to each qubit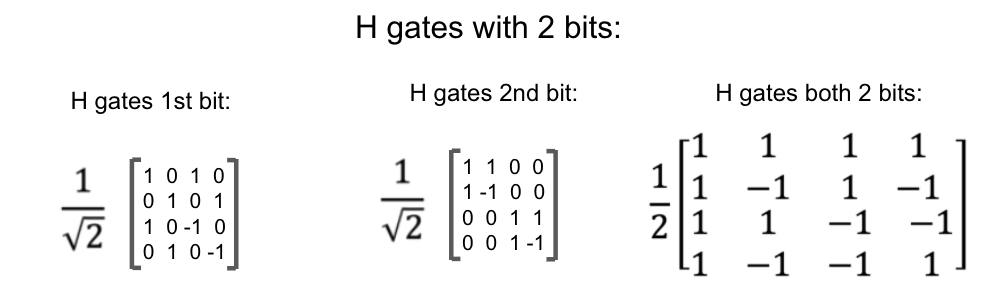
  • public void applyHGate(int qb);
    // apply an H gate to the qubit in position qb, where numbering starts at 0
    // only do so if qb = 0 or 1
  • public void applySwapGate(int qubit1, int qubit2);
    // apply swap gate to the two qubits. Only do so if the two values are 0 and 1

Testing and Submit

We will not require a certain format for testing. Make sure that you test your code thoroughly. Submit once the autograder comes on line.