CS 22880 Week 4
Goals for this homework
- Generalize operations to n bits
- Combining and splitting qubits mathematically
- Using these classes to write algorithms
You are expected to complete this assignment individually. If you need help, you are invited to come to office hours and/or ask questions on Canvas. Clarification questions about the assignments may be asked publicly. Once you have specific bugs related to your code, make the posts private.
In this lab, we are adding the functionality to perform arbitrary operations on multiple qubits using matrix multiplication. In particular, we are generalizing the one- and two-qubit implementations to n qubits.
If you want to add "helper" functions that aren't specified in the assignment, you are welcome to do so. If you want it to be used by all classes, place it in the parent class. If it is specific to a subclass, place it there. We will only test the functions specified, but you're always allowed to add private or protected methods.
You should build off of your last week's assignment. You will add the files NQubit.java, QCircuit.java, QOracle.java.
Set Up
Make sure you add to your Makefile as you complete classes. In addition, you need to create skeletons so that your code will compile properly.
Step 1: NQubit
You will implement NQubit, which applies operations with an arbitrary number of bits. We will only test your code on problems on fairly low numbers of bits, but the code needs to be written in a general way. Like SingleQubit and DoubleQubit, this class is derived from ParentQubit.-
public NQubit(int numqubits);
// Constructor: initialize all bits to 0 -
public ParentQubit mergeQubits(ParentQubit pq);
// this merges two sets of qubits and returns a new one that has
// a number of qubits that is the sum of the two. -
public String toBraKet();
// this prints out the state in bra-ket notation, like last week -
public void applyNotGate();
// apply a not gate to every qubit -
public void applyNotGate(int qb);
// apply a not gate to the qubit in position qb, where numbering starts at 0 -
public void applyHGate();
// apply an H gate to each qubit -
public void applyHGate(int qb);
// apply an H gate to the qubit in position qb, where numbering starts at 0 -
public void applySwapGate(int qubit1, int qubit2);
// apply a swap gate between qubit1 and qubit2, where numbering starts at 0
Step 2: Circuits
The next step is to implement QCircuit. Each method of QCircuit implements a circuit (a sequence of quantum gates). Below, I'll give you the interface and, if the circuit wasn't taught in class, a picture of the circuit. You need to implement that circuit. For the two involving the oracle, read ahead to the Oracle section so that you see what you are calling.
This class has only methods - it has no state. For each method, the state comes in as input arguments and is returned, and there is no reason for it to store anything. Therefore, we will only implement static methods. There is no data stored in this class. You can see how to implement and call static methods here. Specifically, when called, you use the class name rather than a variable name prior to the period (e.g. QCircuit.entangle(...)).
-
public static void sameEntangle(DoubleQubit dq)
// no return value is necessary because you modify the input dq.
-
public static void bernvaz(NQubit nq, QOracle qo)
// You can assume that nq has 4 bits and has been initialized as expected
// for the bernvaz algorithm (3 white, 1 black). qo has already been initialized.
// implement the algorithm.
// no return value is necessary because you modify the input nq.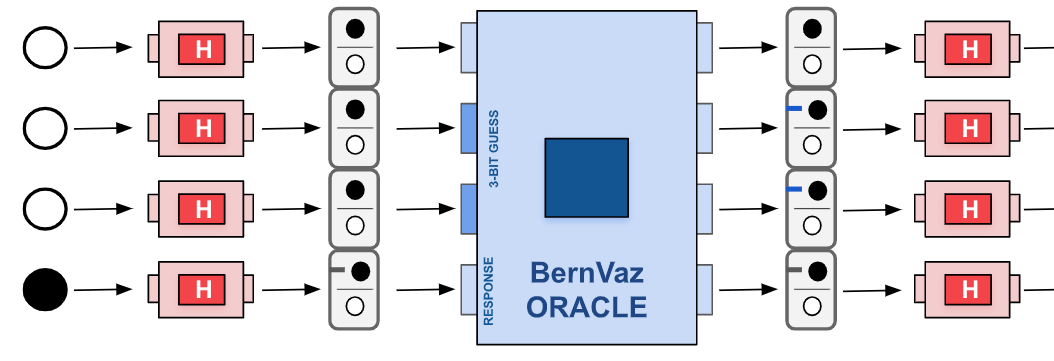
-
public static void archimedes(NQubit nq, QOracle qo)
// You can assume that nq has 4 bits and has been initialized as expected
// for the archimedes algorithm (3 white, 1 black). qo has already been initialized.
// implement the algorithm.
// no return value is necessary because you modify the input nq.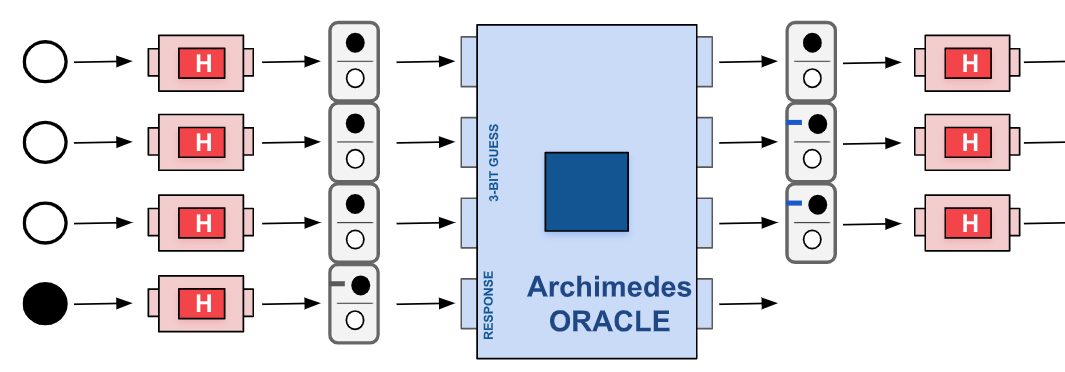
Step 3: Oracles
The next step is to implement QOracle. This implements two oracles: Archimedes and BernVaz.
This class holds the state for two oracles: BernVaz and Archimedes. You need to figure out how, given a code(BernVaz) or set of codes (Archimedes) you can initialize the matrix to implement the desired functionality.
-
public void setBernVaz(int code)
// receives a 3-bit code (number from 0-7). Based on that
// 3-bit code, construct the oracle. For each 1 in the 3-bit code.
// a C-NOT is connected to the response, where the qubit corresponding to
// the 1 is the control, and the response is the target.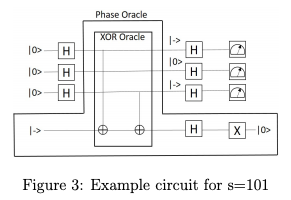
This shows both the algorithm and the oracle. For secret code 101, you can see the C-NOTs that are connected between the response (bottom line) and the top and bottom inputs. This is how quantum circuits are typically depicted (just lines, no solid, colored parts). -
public void probeBernVaz(NQubit nq)
// NQubit is a 4-qubit input, with the first three qubits being the "guess" and
// the last qubit being the response. Apply the oracle. No return value is
// necessary because you modify the state of the input. -
public void setArchimedes(int[] codes)
// receives a set of 3-bit codes (number from 0-7). Based on that
// 3-bit code, construct the oracle. For each 3-bit code, the last
// bit of the input gets flipped. Think carefully about what the matrix looks
// like in the absence of any codes, and then think about how each individual
// code modifies that starting matrix. Once you have figured it out on paper,
// then you can work on how to implement that in code. -
public void probeArchimedes(NQubit nq)
// NQubit is a 4-qubit input, with the first three qubits being the "guess" and
// the last qubit being the response. Apply the oracle. No return value is
// necessary because you modify the state of the input.