Linear Regression

Due: Friday, November 19 at 4:30pm CST.

In this assignment, you will fit linear regression models and implement a few simple feature variable selection algorithms. The assignment will give you experience with NumPy and more practice with using classes and functions to support code reuse.

You must work alone on this assignment.

Getting started

Before you start working on the assignment’s tasks, please take a moment to follow the steps described in Coursework Basics page to get the files for this assignment (these steps will be the same as the ones you followed to get the files previous assignments. Please note that you will not be able to start working on the assignment until you fetch the assignment files (which will appear in a pa5 directory in your repository)

Next, make sure you’ve set the GITHUB_USERNAME variable by running the following (replacing replace_me with your GitHub username):

GITHUB_USERNAME=replace_me

(remember you can double-check whether the variable is properly set by running echo $GITHUB_USERNAME).

And finally, run these commands (if you don’t recall what some of these commands do, they are explained at the end of the Git Tutorial):

cd ~/cmsc12100
mkdir pa5-$GITHUB_USERNAME
cd pa5-$GITHUB_USERNAME
git init
git remote add origin git@github.com:uchicago-cmsc12100-aut-21/pa5-$GITHUB_USERNAME.git
git remote add upstream git@github.com:uchicago-cmsc12100-aut-21/pa5.git
git pull upstream main
git branch -M main
git push -u origin main

You will find the files you need for the programming assignment directly in the root of your repository, including a README.txt file that explains what each file is. Make sure you read that file.

The pa5 directory contains the following files:

regression.py

Python file where you will write your code.

util.py

Python file with several helper functions, some of which you will need to use in your code.

output.py

This file is described in detail in the “Evaluating your model output” section below.

test_regression.py

Python file with the automated tests for this assignment.

The pa5 directory also contains a data directory which, in turn, contains two sub-directories: city and houseprice.

Then as usual, fire up ipython3 from the Linux command-line, set up autoreload, and import your code as follows:

$ ipython3

In [1]: %load_ext autoreload

In [2]: %autoreload 2

In [3]: import util, regression

Data

In this assignment you will write code that can be used on different datasets. We have provided a couple of sample datasets for testing purposes.

City

Predicting crime rate from the number of complaint calls.

House Price

Predicting california house price based on the house features matrix.

More information about each dataset can be found by clicking the links above.

For this assignment, a dataset is stored in a directory that contains two files: a CSV (comma-separated values) file called data.csv and a JSON file called parameters.json. The CSV file contains a table where each column corresponds to a variable and each row corresponds to a sample unit. The first row contains the column names. The JSON file contains a few parameters:

• name: the name of the dataset,

• feature_idx: the column indices of the feature variables,

• target_idx: the column index of the target variable,

• training_fraction: the fraction of the data that should be used to train models, and

• seed: a random number generator seed.

The last two parameters will be used to help split the data into two sets: one that you will use to fit or train models and one that you will use to evaluate how well different models predict outcomes on new-to-the-model data. We describe this process below.

Introduction

In this assignment, you are going to use tabular data (e.g., looks like a table), where each row is a sample unit and each column is a feature of the sample. As an example, in a study to predict California housing price, each sample unit is a house, and each house is represented by features such as house age, number of bedrooms, square feet, etc.

In your analysis, you will build models to predict the target value for each sample unit based on the features representing that sample. For example, you can predict a house’s price (target) based on the house age, number of bedrooms, etc. (features). How you model the relationship between features and the target will affect the prediction accuracy. Building a good prediction model requires selecting related features and applying appropriate algorithms/functions to capture the relationship between features and the target.

As another example, this plot shows th relationship between the number of garbage complaint calls and the number of recorded crimes in that area.

In the above plot, each point is a sample unit that represents a geographical region in Chicago. Each region is associated with several events, such as the number of crimes or the number of garbage complaint calls. Given this plot, if you are asked to predict the number of crimes for a region that had 150 garbage complaint calls, you would follow the general trend and probably say something like 3000 crimes.

To formalize this prediction, we need a model/function to capture the relationship between the target variable (e.g., the number of crimes) and the features (e.g., grabage complaint calls). The above plot shows a linear relationship between the crime rate and the number of complaint calls.

To make this precise, we will use the following notation:

\(N\): the total number of sample units (e.g., data size).

\(K\): the total number of feature variables. In the example above, \(K = 1\) because we use garbage complaint calls as the only feature.

\(n\): the sample unit that we are currently considering (an integer from \(0\) to \(N - 1\)).

\(k\): the index of a feature variable that we are currently considering (an integer from \(0\) to \(K - 1\)).

\(x_{n,k}\): an observation of the feature variable \(k\) of the sample unit \(n\) , e.g., the number of garbage complaint calls from the first region in the city.

\(y_n\): an observation (i.e., the truth) of the target variable for sample unit \(n\), e.g., the total number of crimes in the first region of the city.

\(\hat y_n\): the predicted target variable for sample unit \(n\), based on our observation of the feature variables. This value corresponds to a point on the red line.

\(\varepsilon_n = y_n - \hat y_n\): the residual or observed error, that is, the difference between the actual observed truth value of the target variable, and the prediction for it. Ideally, if the model perfectly fits the data, the model predictions (\(\hat y_n\)) would match the observations (\(y_n\)), so that \(\varepsilon_n\) would be zero. In practice, there will be some differences for several reasons. First, there may be noise in our data, which arises from errors measuring the features or target variables. Additionally, our model will assume a linear dependence between the feature variables and the target variable, while in reality the relationship is unlikely to be exactly linear. However, linear models are in general a good fit to a wide variety of real-world data, and are an appropriate baseline to consider before moving on to more advanced models.

We will use the following linear equation to calculate the prediction for target variable (\(\hat y_n\)) based on the feature variables (\(x_nk\)) for the sample unit \(n\) as:

(1)\[\hat y_n = \beta_0 + \beta_1 x_{n1} + \dots + \beta_K x_{n,K},\]

where the coefficients \(\beta_0, \beta_1, \dots, \beta_K\) are model parameters (real numbers that are internal to the model). We would like to select values for these coefficients that result in small errors \(\varepsilon_n\).

We can rewrite this equation more concisely using vector notation. We define:

\(\newcommand{\vbeta}{\pmb{\beta}} \vbeta = \begin{pmatrix} \beta_0 & \beta_1 & \beta_2 & \cdots & \beta_K\end{pmatrix}^T\)

a column vector of the model parameters, where \(\beta_0\) is the intercept and \(\beta_k\) (for \(1 \leq k \leq K\)) is the coefficient associated with feature variable \(k\). This vector describes the red line in the figure above. Note that a positive value of a coefficient suggests a positive correlation between the target variable and the feature variable. The same is true for a negative value and a negative correlation.

\(\mathbf{x}_n = \begin{pmatrix} 1 & x_{n1} & x_{n2} & \cdots & x_{n,K}\end{pmatrix}^T\)

a row vector representation of all the features for a given sample unit \(n\). Note that a 1 has been prepended to the vector. This will allow us to rewrite equation (1) in vector notation without having to treat \(\beta_0\) separately from the other coefficients \(\beta_k\).

We can then rewrite equation (1) as:

(2)\[\hat y_n = \mathbf{x}_n^T \vbeta.\]

This equation can be written for all sample units at the same time using matrix notation. We define:

\(\newcommand{\vy}{\mathbf{y}} \vy = \begin{pmatrix} y_0 & y_1 & \cdots & y_{N - 1}\end{pmatrix}^T\)

a column vector of truth observations of the target variable.

\(\newcommand{\vyhat}{\mathbf{\hat y}} \vyhat = \begin{pmatrix} \hat y_0 & \hat y_1 & \cdots & \hat y_{N - 1}\end{pmatrix}^T\)

a column vector of predictions for the target variable.

\(\newcommand{\veps}{\pmb{\varepsilon}} \veps = \begin{pmatrix} \varepsilon_0 & \varepsilon_1 & \cdots & \varepsilon_{N - 1}\end{pmatrix}^T\)

a column vector of the observed errors.

\(\mathbf{X}\): an \(N \times (K + 1)\) matrix where each row is one sample unit. The first column of this matrix is all ones, and the remaining \(K\) columns correspond to the \(K\) features.

We can then write equations (1) and (2) for all sample units at once as

(3)\[\mathbf{\hat y} = \mathbf{X} \vbeta,\]

And, we can express the residuals as

(4)\[\veps = \vy - \vyhat.\]

Matrix multiplication

Equations (2) and (3) above involve matrix multiplication. If you are unfamiliar with matrix multiplication, you will still be able to do this assignment. Just keep in mind that to make the calculations less messy, the matrix \(\mathbf{X}\) contains not just the observations of the feature variables, but also an initial column of all ones. The data we provide does not yet have this column of ones, so you will need to prepend it.

Model fitting

There are many possible candidate values for \(\vbeta\), some fit the data better than others. The process of finding the appropriate value for \(\vbeta\) is referred to as fitting the model. For our purposes, the “best” value of \(\vbeta\) is the one that minimizes the errors \(\veps = \vy - \vyhat\) in the least-squared sense. That is, we want the predicted values \(\vyhat\) to be as close to the observed values \(\vy\) as possible (i.e., we want \(\abs(\vy - \vyhat)\) to be as small as possible), where the predicted values are calculated as \(\mathbf{\hat y} = \mathbf{X} \vbeta\). We provide a linear_regression function, described below, that computes \(\vbeta\).

The linear_regression function

We are interested in the value of \(\vbeta\) that best fits the data. To simplify your job, we have provided code for fitting a linear model. The function linear_regression(X, y) in util.py finds the best value of \(\vbeta\). This function accepts a two-dimensional NumPy array X of floats containing the observations of the feature variables (\(\mathbf{X}\)) and a one-dimensional NumPy array y of floats containing the observations of the target variable (\(\vy\)). It returns \(\vbeta\) as a one-dimensional NumPy array beta.

We have also provided a function, apply_beta(beta, X) for making predictions using the linear regression model. It takes beta, the array generated by our linear regression function, and X as above, applies the linear function described by beta to each row in X, and returns a one-dimensional NumPy array of the resulting values (that is, it returns \(\mathbf{X} \vbeta\)).

The data we provide only has \(K\) columns, corresponding to the \(K\) features; it does not have the leading column of all ones. Before calling linear_regression(X, y), we need to construct the matrix X by prepending a column of ones to our data. This column of ones allows the linear regression model to fit an intercept \(\beta_0\) as discussed above. We have provided a function prepend_ones_column(A) to do so.

Here are sample calls to prepend_ones_column, linear_regression, apply_beta:

In [1]: import numpy as np

In [2]: import util

In [3]: features = np.array([[5, 2], [3, 2], [6, 2.1], [7, 3]])

In [4]: X = util.prepend_ones_column(features)

In [5]: X
Out[5]:
array([[1. , 5. , 2. ],
    [1. , 3. , 2. ],
    [1. , 6. , 2.1],
    [1. , 7. , 3. ]])

In [6]: y = np.array([5, 2, 6, 6]) # observations of target variable

In [7]: beta = util.linear_regression(X, y)

In [8]: beta
Out[8]: array([ 1.20104895,  1.41083916, -1.6958042 ])

In [9]: util.apply_beta(beta, X) # yhat_n = 1.20 + 1.41 * x_n1 - 1.69 * x_n2
Out[9]: array([4.86363636, 2.04195804, 6.1048951 , 5.98951049])

Task 0: The Model class

In this assignment, you will be working with datasets and models, so it will make sense for us to have a DataSet class and a Model class. We provide the Dataset class and the basic skeleton of the Model class in regression.py.

This section describes the requirements for the Model and DataSet classes. While you should give some thought to the design of these classes before moving on to the rest of the assignment, it is very likely you will have to reassess your design throughout the assignment (and you should not get discouraged if you find yourself doing this). We suggest you start by writing first drafts of the Model and DataSet classes, and then fine-tune these drafts as you work through the rest of the assignment.

Representing datasets

The DataSet class (that we provide for you) handles loading in the data files described above (CSV and JSON). It reads the data into a Numpy array and uses the JSON format to set various attributes. Additionally, it partitions the data into two different numpy arrays, a training_data array and a testing_data array. We will use the training_data array to train the model and then test the model performance on the testing_data array.

A standard pipeline for training and evaluating a model is to first fit the model with training data, and then to evaluate the model performance on testing data. The testing data are held-out data that the model didn’t see during training. A good model is a model that fits the training data well and also performs well on previously unseen testing data.

Representing models

Implementing a Model class will allow us to encapsulate the data and operations as a whole. That is, the Model class will allow us to write functions that take Model objects as parameters and return Model objects as well. Instead of passing around lists or dictionaries we can directly pass objects to a given model.

We will construct a model using a dataset and a subset of the feature variables, which means your Model class will take a dataset and a list of feature indices as arguments to its constructor. We encourage you to think carefully about what attributes and methods to include in your class.

Your Model class must have at least the following public attributes (don’t worry if you don’t understand what these mean right now; they will become clearer in subsequent tasks):

• target_idx: The index of the target variable.

• feature_idx: A list of integers containing the indices of the feature variables.

• beta: A NumPy array with the model’s \(\vbeta\)

These attributes need to be present for the automated tests to run. To compute beta you will use the linear_regression function that we discuss above. And it can be very helpful to include a __repr__ method.

Testing your code

As usual, you will be able to test your code from IPython and by using py.test. When using IPython, make sure to enable autoreload before importing the regression.py module:

In [1]: %load_ext autoreload

In [2]: %autoreload 2

In [3]: import regression

You might then try creating a new Model object by creating a DataSet object (let’s assume we create a dataset variable for this) and running the following:

In [3]: dataset = regression.DataSet('data/city')

In [4]: model = regression.Model(dataset, [0, 1, 2])

You can also use the automated tests. For example, you might run:

$ py.test -vk task0

A note on array dimensions

The parameter of the function prepend_ones_column (as well as the first parameter to the functions linear_regression and apply_beta described below) is required to be a two-dimensional array, even when that array only has one column. NumPy makes a distinction between one-dimensional and two-dimensional arrays, even if they contain the same information. For instance, if we want to extract the second column of A as a one-dimensional array, we do the following:

In [5]: A
Out[5]: array([[5. , 2. ],
               [3. , 2. ],
               [6. , 2.1],
               [7. , 3. ]])
In [6]: A[:, 1]
Out[6]: array([2. , 2. , 2.1, 3. ])

In [7]: A[:, 1].shape
Out[7]: (4,)

The resulting shape will not be accepted by prepend_ones_column. To retrieve a 2D column subset of A, you can use a list of integers as the index. This mechanism keeps A two-dimensional, even if the list of indices has only one value:

In [8]: A[:, [1]]
Out[8]: array([[2. ],
               [2. ],
               [2.1],
               [3. ]])
In [9]: A[:, [1]].shape
Out[9]: (4, 1)

In general, you can specify a slice containing a specific subset of columns as a list. For example, let Z be:

In [10]: Z = np.array([[1, 2, 3, 4], [11, 12, 13, 14], [21, 22, 23, 24]])
In [11]: Z
Out[11]: array([[ 1,  2,  3,  4],
                [11, 12, 13, 14],
                [21, 22, 23, 24]])

Evaluating the expression Z[:, [0, 2, 3]] will yield a new 2D array with columns 0, 2, and 3 from the array Z:

In [12]: Z[:, [0, 2, 3]]
Out[12]: array([[ 1,  3,  4],
                [11, 13, 14],
                [21, 23, 24]])

or more generally, we can specify any expression for the slice that yields a list:

In [13]: l = [0, 2, 3]
In [14]: Z[:, l]
Out[14]: array([[ 1,  3,  4],
                [11, 13, 14],
                [21, 23, 24]])

Task 1: Computing the coefficient of Determination (R²)

Blindly regressing on all available features is bad practice and can lead to over-fit models. Over-fitting happens when your model picks up a structure that fits well on your training data but not generalize to unseen data. Which means, the model only captures the specific underlying phenomenon in that specific training data, but this phenomenon is not commonly exist in other data. (Wikipedia has a nice explanation ). This situation is made even worse if some of your features are highly correlated (see multicollinearity), since it can ruin the interpretation of your coefficients. As an example, consider a study that looks at the effects of smoking and drinking on developing lung cancer. Smoking and drinking are highly correlated, so the regression can arbitrarily pick up either as the explanation for high prevalence of lung cancer. As a result, drinking could be assigned a high coefficient while smoking a low one, leading to the questionable conclusion that drinking is more correlated with lung cancer than smoking.

This example illustrates the importance of feature variable selection. In order to compare two different models (subsets of features) against each other, we need a measurement of their goodness of fit, i.e., how well they explain the data. A popular choice is the coefficient of determination, R², which first considers the variance of the target variable, \(\DeclareMathOperator{\Var}{Var} \Var(\vy)\):

In this example we revisit the regression of the total number of crimes, \(y_n\), on the number of calls about garbage to 311, \(x_n\). To the right, a histogram over the \(y_n\) is shown and their variance is calculated. The variance is a measure of how spread out the data is. It is calculated as follows:

(5)\[\Var(\vy) = \frac{1}{N}{\sum_{n=1}^N} (y_n - \bar y)^2,\]

where \(\bar y\) denotes the mean of all of the \(y_n\).

We now subtract the red line from each point. These new points are the residuals and represent the deviations from the predicted values under our model. If the variance of the residuals, \(\Var(\vy - \vyhat),\) is zero, it means that all residuals have to be zero and thus all sample units lie perfectly on the fitted line. On the other hand, if the variance of the residuals is the same as the variance of \(\vy\), it means that the model did not explain anything away and we can consider the model useless. These two extremes represent R² values of 1 and 0, respectively. All R² values in between these two extremes will be cases where the variance was reduced some, but not entirely. Our example is one such case:

As we have hinted, the coefficient of determination, R², measures how much the variance was reduced by subtracting the model. More specifically, it calculates this reduction as a percentage of the original variance:

(6)\[R^2 = \frac{\Var(\vy) - \Var(\vy - \vyhat)}{\Var(\vy)} = 1 - \frac{\Var(\vy - \vyhat)}{\Var(\vy)}.\]

which finally becomes:

(7)\[R^2 = 1 - \frac{\sum_{n=1}^N (y_n - \hat y_n)^2}{\sum_{n=1}^N (y_n - \bar y)^2}.\]

In equation (7) we omitted the normalization constants N since they cancel each other out. We also did not subtract the mean when calculating the variance of the residuals, since it can be shown mathematically that if the model has been fit by least squares, the sum of the residuals is always zero.

There are two properties of R² that are good to keep in mind when checking the correctness of your calculations:

1. \(0 \leq R^2 \leq 1\).

2. If model A contains a superset of features of model B, then the R² value of model A is greater than or equal to the R² value of model B.

These properties are only true if R² is computed using the same data that was used to train the model parameters. If you calculate R² on a held-out testing set, the R² value could decrease with more features (due to over-fitting) and R² is no longer guaranteed to be greater than or equal to zero. Furthermore, equations (6) and (7) would no longer be equivalent (and the intuition behind R² would need to be reconsidered, but we omit the details here). You should always use equation (7) to compute R².

A good model should explain as much of the variance as possible, so we will be favoring higher R² values. However, since using all features gives the highest R², we must balance this goal with a desire to use few features. In general it is important to be cautious and not blindly interpret R²; take a look at these two generated examples:

This data was generated by selecting points on the dashed blue function, and adding random noise. To the left, we see that the fitted model is close to the one we used to generate the data. However, the variance of the residuals is still high, so the R² is rather low. To the right is a model that clearly is not right for the data, but still manages to record a high R² value. This example also shows that that linear regression is not always the right model choice (although, in many cases, a simple transformation of the features or the target variable can resolve this problem, making the linear regression paradigm still relevant).

Task 1

Add the following attribute to your model class:

• R2: The value of R² for the model

and compute it. Note that when we ask for the R² value for a model, we mean the value obtained by computing R² using the model’s \(\vbeta\) on the data that was used to train it.

Note

You may not use the NumPy var method to compute R² for two reasons: (1) our computation uses the biased variance while the var method computes the unbiased variance and will lead you to generate the wrong answers and (2) we want you to get practice working with NumPy arrays.

Task 2: Model evaluation using the Coefficient of Determination (R²)

Task 2a

Implement this function in regression.py:

def compute_single_var_models(dataset):
    '''
    Computes all the single-variable models for a dataset

    Inputs:
        dataset: (DataSet object) a dataset

    Returns:
        List of Model objects, each representing a single-variable model
    '''

More specifically, given a dataset with P feature variables, you will construct P univariate (i.e., one variable) models of the dataset’s target variable, one for each of the possible feature variables (in the same order that the target variables are listed), and compute their associated R² values.

Most of the work in this task will be in your Model class. In fact, if you’ve designed Model correctly, your implementation of compute_single_var_models shouldn’t be longer than three lines (ours is actually just one line long).

Task 2b

Implement this function in regression.py:

def compute_all_vars_model(dataset):
    '''
    Computes a model that uses all the feature variables in the dataset

    Inputs:
        dataset: (DataSet object) a dataset

    Returns:
        A Model object that uses all the feature variables
    '''

More specifically, you will construct a single model that uses all of the dataset’s feature variables to predict the target variable. According to the second property of R², the R² for this model should be the largest R² value you will see for the training data.

At this point, you should make sure that your code to calculate a model’s R² value is general enough to handle models with multiple feature variables (i.e., multivariate models).

Take into account that, if you have a good design for Model, then implementing Task 2b should be simple after implementing Task 2a. If it doesn’t feel that way, ask on Ed Discussion or come to office hours so we can give you some quick feedback on your design.

Evaluating your model output

Note that IPython can be incredibly helpful when testing Task 2 and subsequent tasks. For example you can test Task 2a code by creating a DataSet object (let’s assume we create a dataset variable for this) and running the following:

In [3]: dataset = regression.DataSet('data/city')
In [4]: univar_models = regression.compute_single_var_models(dataset)

univar_models should then contain a list of Model objects. However, checking the R² values manually from IPython can be cumbersome, so we have included a Python program, output.py, that will print out these (and other) values for all of the tasks. You can run it from the command-line like this:

$ python3 output.py data/city

If your implementation of Task 2a is correct, you will see this:

City Task 2a
    !!! You haven't implemented the Model __repr__ method !!!
    R2: 0.1402749161031348

    !!! You haven't implemented the Model __repr__ method !!!
    R2: 0.6229070858532733

    !!! You haven't implemented the Model __repr__ method !!!
    R2: 0.5575360783921093

    !!! You haven't implemented the Model __repr__ method !!!
    R2: 0.7831498392992615

    !!! You haven't implemented the Model __repr__ method !!!
    R2: 0.7198560514392482

    !!! You haven't implemented the Model __repr__ method !!!
    R2: 0.32659079486818354

    !!! You haven't implemented the Model __repr__ method !!!
    R2: 0.6897288976957778

You should be producing the same R² values shown above, but we can’t tell what model they each correspond to! For output.py to be actually useful, you will need to implement the __repr__ method in Model.

We suggest your string representation be in the following form: the name of the target variable followed by a tilde (~) and the regression equation with the constant first. If you format the floats to have six decimal places, the output for Task 2a will now look like this:

City Task 2a
    CRIME_TOTALS ~ 575.687669 + 0.678349 * GRAFFITI
    R2: 0.1402749161031348

    CRIME_TOTALS ~ -22.208880 + 5.375417 * POT_HOLES
    R2: 0.6229070858532733

    CRIME_TOTALS ~ 227.414583 + 7.711958 * RODENTS
    R2: 0.5575360783921093

    CRIME_TOTALS ~ 11.553128 + 18.892669 * GARBAGE
    R2: 0.7831498392992615

    CRIME_TOTALS ~ -65.954319 + 13.447459 * STREET_LIGHTS
    R2: 0.7198560514392482

    CRIME_TOTALS ~ 297.222082 + 10.324616 * TREE_DEBRIS
    R2: 0.32659079486818354

    CRIME_TOTALS ~ 308.489056 + 10.338500 * ABANDONED_BUILDINGS
    R2: 0.6897288976957778

For example, the first model uses only one feature variable, GRAFFITI to predict crime, and has an R² of only 0.14027. The last model uses only ABANDONED_BUILDINGS, and the higher R² (0.6897) tells us that ABANDONED_BUILDINGS is likely a better feature than GRAFFITI.

Take into account that you can also run output.py with the House Price dataset:

$ python3 output.py data/houseprice

The full expected output of output.py can be found in the City and House Price pages. However, please note that you do not need to check all this output manually. We have also included automated tests that will do these checks for you. You can run them using this command:

$ py.test -vk task2

Warning: No hard-coding!

Since we only have two datasets, it can be very easy in some tasks to write code that will pass the tests by hard-coding the expected values in the function (and returning one or the other depending on the dataset that is being used)

If you do this, you will receive a U as your completeness score, regardless of whether other tasks are implemented correctly without hard-coding

Task 3: Building and selecting bivariate models

If you look at the output for Task 2a, none of the feature variables individually are particularly good features for the target variable (they all had low R² values compared to when using all features). In this and subsequent tasks, we will construct better models using multiple feature variables without using all of them and risking over-fitting.

For example, we could predict crime using not only complaints about garbage, but graffiti as well. For example, we may want to find \(\vbeta = (\beta_0, \beta_\texttt{GARBAGE}, \beta_\texttt{GRAFFITI})\) in the equation

\[\hat y_n = \beta_0 + \beta_\texttt{GARBAGE} x_{n \, \texttt{GARBAGE}} + \beta_\texttt{GRAFFITI} x_{n \, \texttt{GRAFFITI}},\]

where \(\hat y_n\) is a prediction of the number of crimes given the number of complaint calls about garbage (\(x_{n \, \texttt{GARBAGE}}\)) and graffiti (\(x_{n \, \texttt{GRAFFITI}}\)).

For this task, you will test all possible bivariate models (\(K = 2\)) and determine the one with the highest R² value. We suggest that you use two nested for-loops to iterate over all possible combinations of two features, calculate the R² value for each combination and keep track of one with the highest R² value.

Hint: Given three feature variables A, B, C, we only need to check (A, B), (A, C), and (B, C). Take into account that a model with the pair (A, B) of variables is the same as the model with (B, A).

To do this task, you will implement this function in regression.py:

def compute_best_pair(dataset):
    '''
    Find the bivariate model with the best R2 value

    Inputs:
        dataset: (DataSet object) a dataset

    Returns:
        A Model object for the best bivariate model
    '''

Unlike the functions in Task 2, you can expect to write more code in this function. In particular, you should not include the code to loop over all possible bivariate models within your Model class; it should instead be in this function.

You can test this function by running:

$ py.test -vk task3

You should also look at the output produced by output.py. How does the bivariate model compare to the single-variable models in Task 2? Which pair of feature variables perform best together? Does this result make sense given the results from Task 2? (You do not need to submit your answers to these questions; they’re just food for thought!)

Task 4: Building models of arbitrary complexity

How do we efficiently determine how many and which feature variables will generate the best model? It turns out that this question is unsolved and is of interest to both computer scientists and statisticians. To find the best model of three feature variables we could repeat the process in Task 3 with three nested for-loops instead of two. For K feature variables we would have to use K nested for-loops. Nesting for-loops quickly becomes computationally expensive and infeasible for even the most powerful computers. Keep in mind that models in genetics research easily reach into the thousands of feature variables. How then do we find optimal models of several feature variables?

We’ll approach this problem by using heuristics, which will give us an approximate (as opposed to an exact) result. We are going to split this problem into two tasks. In Task 4, you will determine the best K feature variables to use (for each possible value of K).

How do we determine which K feature variables will yield the best model for a fixed K? As noted, the naive approach (test all possible combinations as in Task 3), is intractable for large K. An alternative simpler approach is to choose the K feature variables with the K highest R² values in the table from Task 2a. This approach does not work well if your features are correlated. As you’ve already seen, neither of the top two individual features for crime (GARBAGE and STREET_LIGHTS) are included in the best bivariate model (CRIME_TOTALS ~ -36.151629 + 3.300180 * POT_HOLES + 7.129337 * ABANDONED_BUILDINGS).

Instead, you’ll implement a heuristic known as Forward selection, which is an example of a greedy algorithm. Forward selection starts with an empty set of feature variables and then adds one at a time until the set contains K feature variables. At each step, the algorithm identifies the feature variable in the model that, when added, yields the model with the best R² value. That feature variable is added to the list of feature variables.

To do this task, you will implement this function in regression.py:

def forward_selection(dataset):
  '''
  Given a dataset with P feature variables, uses forward selection to
  select models for every value of K between 1 and P.

  Inputs:
      dataset: (DataSet object) a dataset

  Returns:
      A list (of length P) of Model objects. The first element is the
      model where K=1, the second element is the model where K=2, and so on.
  '''

You can test this function by running this:

$ py.test -vk task4

A word of caution

In this task, you have multiple models, each with their own list of feature variables. Recall that lists are stored by reference, so a bug in your code might lead to two models pointing to the same list! These sorts of bugs can be very tricky to debug, so remember to be careful.

Feature standardization

Feature standardization is a common pre-processing step for many statistical machine learning algorithms. In the dataset, each sample is represented by multiple features and each feature might have a different range. For example, in the California house price prediction task, the values for the feature median house age in block group ranges from 2 to 52, and the values for the feature average number of rooms per household ranges from 2.65 to 8.93. We want to standardize the data such that each feature has a mean of zero and standard deviation of one. After standardization, we can then fairly compare the coefficient of each feature and features with large coefficients are “important” than those with small coefficients. However, if we don’t do feature standardization, feature coefficients are not necessarilly comparable.

We have provided a function called standardize_features() in the DataSet class in regression.py. The decision of whether or not to standardize features is controlled by the model parameters specified in the data/city/parameters.json or data/houseprice/parameters.json files. The default setting is “standardization”: “no”, which means the data is not standardized. You can change “no” to “yes” to standardize the data and then pass the standardized data to the training algorithm.

Previously, you were running your code under the default setting (“no”), so the results you have seen are without standardization. For now, please change the setting to “standardization”: “yes”, and re-run the previous experiments with standardized data. You can do so by running:

$ python3 output.py data/city

The full expected output can be found in the City and House Price pages.

Now, you have results without data standardization and results with data standardization. When you compare the differences between the outputs under the two settings, you can see that the models trained with standardized data have smaller ranges of the \(\beta\) values, especially \(\beta_0\) (i.e., the intercept). This is because when the feature values are standardized in the same range, the model no longer needs large intercept to adjust for the large discrepancy of different feature values.

Task 5: Training vs. testing data

Please read this section very carefully

Before implementing this step, please remember to change the parameter setting in parameters.json back to “standardization”: “no”.

Until now, you have evaluated a model using the data that was used to train it. The resulting model may be quite good for that particular dataset, but it may not be particularly good at predicting novel data. This is the problem that we have been referring to as over-fitting.

Up to this point, we have only computed R² values for the training data that was used to construct the model. That is, after training the model using the training data, we used that same data to compute an R² value. It is also valid to compute an R² value for a model when applied to other data (in our case, the data we set aside as testing data). When you do this, you still train the model (that is, you compute \(\vbeta\)) using the training data, but then evaluate an R² value using the testing data.

Note: in the Dataset class, we have provided code that splits the data into training and testing using train_test_split method from the sklearn package, with a training_fraction specified in the parameters.json file.

Warning

When training a model, you should only ever use the training data, even if you will later evaluate the model using other data. You will receive zero credit for this task if you train a new model using the testing data.

To do this task, you will implement the following function in regression.py. We will apply this function to evaluate the models generated in Task 4.

def validate_model(dataset, model):
    '''
    Given a dataset and a model trained on the training data,
    compute the R2 of applying that model to the testing data.

    Inputs:
        dataset: (DataSet object) a dataset
        model: (Model object) A model that must have been trained
           on the dataset's training data.

    Returns:
        (float) An R2 value
    '''

If your Model class is well designed, this function should not require more than one line (or, at most, a few lines) to implement. If that is not the case, please come to office hours or ask on Ed Discussion so we can give you some quick feedback on your design.

You can test this function by running this:

$ py.test -vk task5

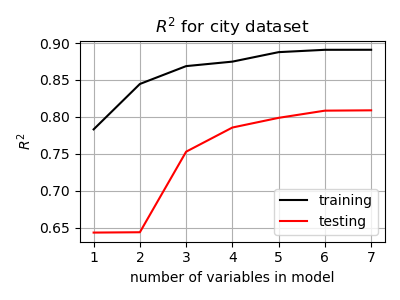
We can see below how the training versus testing R² value increases as we add more feature variables to our model for the City dataset. There are two interesting trends visible in these curves.

• The R² for the test set is consistently lower than the training set R². Our model performs worse at predicting new data than it did on the training data. This is a common feature when training models with data, and is to be expected (why?).

• The improvement in R² slows as we add more feature variables. In essence, the first few varibles provide a lot of predictive power, but each additional feature variable explains less and less. For some datasets (not the small ones in this exercise), it’s possible to add so many feature variables that the R² of the test set starts to decrease! This is the essence of “over-fitting” : building a model that fits the training set too closely, and does not work well on novel (test) data.

Slight numerical errors

If you are consistently getting answers that are “close” but not correct, you may have inadvertently used the wrong equation. Make sure you are using (7) to compute R² and the associated variance.

Grading

The assignment will be graded according to the Rubric for Programming Assignments. Make sure to read that page carefully.

In particular, your completeness score will be determined solely on the basis of the automated tests, which provide a measure of how many of the tasks you have completed:

Grade	Percent tests passed
Exemplary	at least 95%
Satisfactory	at least 80%
Needs Improvement	at least 60%
Ungradable	less than 60%

For example, if your implementation passes 85% of the tests, you will earn an S (satisfactory) score for completeness.

The code quality score will be based on the general criteria in the Rubric for Programming Assignments. And don’t forget that style also matters! Make sure to review the general guidelines in the Rubric for Programming Assignments, as well as our Style Guide.

Cleaning up

Before you submit your final solution, you should, remove

• any print statements that you added for debugging purposes and

• all in-line comments of the form: “YOUR CODE HERE” and “REPLACE …”

Also, check your code against the style guide. Did you use good variable and function names? Do you have any lines that are too long? Did you remember to include a header comment for all of your functions?

Do not remove header comments, that is, the triple-quote strings that describe the purpose, inputs, and return values of each function.

As you clean up, you should periodically save your file and run your code through the tests to make sure that you have not broken it in the process.

Submission

You will be submitting your work through Gradescope (linked from our Canvas site). The process will be the same as with previous coursework: Gradescope will fetch your files directly from your PA5 repository on GitHub, so it is important that you remember to commit and push your work! You should also get into the habit of making partial submissions as you make progress on the assignment; remember that you’re allowed to make as many submissions as you want before the deadline.

To submit your work, go to the “Gradescope” section on our Canvas site. Then, click on “Programming Assignment #5”. If you completed previous assignments, Gradescope should already be connected to your GitHub account. If it isn’t, you will see a “Connect to GitHub” button. Pressing that button will take you to a GitHub page asking you to confirm that you want to authorize Gradescope to access your GitHub repositories. Just click on the green “Authorize gradescope” button.

Then, under “Repository”, make sure to select your uchicago-cmsc12100-aut-21/pa5-$GITHUB_USERNAME.git repository. Under “Branch”, just select “main”.

Finally, click on “Upload”. An autograder will run, and will report back a score. Please note that this autograder runs the exact same tests (and the exact same grading script) described in Testing Your Code. If there is a discrepancy between the tests when you run them on your computer, and when you submit your code to Gradescope, please let us know.