“The Markovian Candidate”: Speaker Attribution Using Markov Models¶
Due: Friday, January 21st at 4:30pm
The goal of this assignment is to give you practice with building a hash table from scratch, s and to exercise the skills you learned in module
You must work alone for this assignment.
Introduction¶
Module #1, we also talked about hash tables: data structures that store associations between keys and values (exactly like dictionaries in Python) and provide an efficient means of looking up the value associated with a given key. Hash tables find a desired entry rapidly by limiting the set of places where it can be. They avoid “hot spots,” even with data that might otherwise all seem to belong in the same place, by dispersing the data through hashing.
These benefits are why Python, in fact, uses hash tables behind the scenes in its implementation of dictionaries. The concept of hashing is so fundamental and useful in so many ways, however, that now is the time to peel back the curtain and see how dictionaries work by building your own. That is the other objective of this assignment.
Apart from developing an appreciation of how hashing and hash tables work, you will also be better prepared if ever you need to write your own hash table in the future. For instance, you may use a language (like C) that does not feature a built-in hash table. Or, the hash table that is used by a language, like Python, may interact poorly with your particular data, obligating you to design a custom-tailored one. After completing this assignment, you should consider hash tables to be in your programming repertoire.
We will use these hash tables to explore our first data analysis concept, Markov Models. We will learn more about them later in the course but for now Markov models can capture the statistical relationships present in a language like English, which we will be using to implement a speaker attribution application.
Getting started¶
Please make sure to watch the following module videos before beginning this pa:
1.2 - Command Line Arguments
1.3 - Introduction to Hash tables
Using the invitation URL provided on Ed Discussion, create a repository for your PA #1 files.
When you click on an invitation URL, you will have to complete the following steps:
You will need to select your CNetID from a list. This will allow us to know what student is associated with each GitHub account. This step is only done for the very first invitation you accept.
You must click “Accept this assignment” or your repository will not actually be created.
After accepting the assignment, Github will take a few minutes to create your repository. You should receive an email from Github when your repository is ready. Normally, it’s ready within seconds and you can just refresh the page.
For the remainder of the quarter, you should place all repositories in a single directory. Many of you may have already done this but you can make a CAPP 122 directory as follows:
mkdir capp30122
Next, make sure you’ve
set the GITHUB_USERNAME variable by running the following (replacing replace_me
with your GitHub username):
GITHUB_USERNAME=replace_me
(remember you can double-check whether the variable is properly set by
running echo $GITHUB_USERNAME)
And finally, run these commands (if you don’t recall what some of these commands do, they are explained at the end of the Git Tutorial):
cd ~/capp30122
mkdir pa1-$GITHUB_USERNAME
cd pa1-$GITHUB_USERNAME
git clone git@github.com:uchicago-CAPP30122-win-2022/pa1-$GITHUB_USERNAME.git
You will find the files you need for the programming assignment directly in the root of your repository. The next section will describe more details about the structure of the repository.
Task #1: Setup the Speaker Recognition Project¶
Your first task is to setup the Speaker Recognition Project, as described in module #1. We have already provided the files and directories in the correct structure in your repositories; however, you need to add additional files and code (i.e., the correct import statements) to make the project fully complete. For this PA, the following should be the packages:
top-level package: The application will be under the package
markovianand will be executed with this name. We describe how to execute this application in the sections below. You need to add the necessary file(s) to makemarkovianthe top-level package as described in module 1. The entry-point into the application is theapp.runfunction.subpackages: The project should have the directoires
collections,models, andtests. You need to add the necessary file(s) to make them into subpackages of themarkoviantop-level package.The
datadirectory is not a package. You must leave it as is. It contains the speech data that you will need in the later sections of the PA.
As you implement this assignment, you will need to update the modules with the correct import statements to make sure you are correctly importing the subpackages and modules.
Please note your code will fail without including the correct import statements.
Task #2: Hash tables and Linear Probing¶
In the interest of building and testing code one component at a time, you will start by building a hash table. Once you have gotten this module up and running, you will use it in your construction of a Markov model for speaker attribution.
There are different types of hash tables; for this assignment, we will use the type that is implemented with linear probing. We described how these work in Module #1; here is another reference on the topic.
Please look at /markovian/collections/lp.py. You will modify this file to implement a hash table using the linear probing algorithm. The class LPHashtable must have:
It must implement the abstract class defined in
/markovian/collections/hash_table.py. This requirement means you will need to implement the abstract methods inLPHashtable. We explain those implementations below.A hash function that takes in a string and returns a hash value. Use the standard string hashing function discussed in class. This function should be “private” to the class. A private method is one that begins with a underscore (i.e.,
_).A constructor that takes in the initial number of cells to use and a default value, of your choosing, to return when looking up a key that has not been inserted. It must create a list of empty cells with the specified length. You can assume the value passed in for the initial number of cells will be greater than 0.
__getitem__, which takes in a key and returns its associated value: either the one stored in the hash table, if present, or the default value, if not.__setitem__, which takes in a key and value, and updates the existing value for that key with the new value or inserts the key-value pair into the hash table, as appropriate.__contains__, which takes in a key and returnsTrueif the key is inside the hash table; otherwise, returnFalse.
A hash table built on linear probing does not have unlimited capacity, since each cell can only contain a single value and there are a fixed number of cells. But, we do not want to have to anticipate how many cells might be used for a given hash table in advance and hard-code that number in for the capacity of the hash table. Therefore, we will take the following approach: the cell capacity passed into the constructor will represent the initial size of the table. If the fraction of occupied cells grows beyond the constant TOO_FULL after an update, then we will perform an operation called rehashing: We will expand the size of our hash table, and migrate all the data into their proper locations in the newly-expanded hash table (i.e., each key-value pair is hashed again, with the hash function now considering the new size of the table). We will grow the size of the table by GROWTH_RATIO; for instance, if this is 2, the size of the hash table will double each time it becomes too full. The constants are already defined in the lp.py file for you.
You must use the hash function presented in these http://www.cs.princeton.edu/courses/archive/spr03/cs226/lectures/hashing.4up.pdf slides, and use 37 as a constant prime multiplier in that function. Use the ord() function in Python to compute the numerical value of a character. Let \(f()\) be a function that maps a character \(c_i\) in a string \(S=c_1c_2...c_j\) to a number, \(k=37\) a constant, and \(M\) as the size of the hash table, then a possible hash function \(h()\), which you must use in this assignment, can be defined as (see slide #6):
and
where \(g(c_i)\) is the function that actually computes the integer index for all characters in the string \(S\).
Testing - We have provided test code for your hash table class in /markovian/tests/test_hash_table.py.
Note
You will most likely only use the __getitem__ and __setitem__ methods in the following sections. However, the __contains__ method is there so you can get practice building a more complex data structure that uses the built-in operators of Python.
A Speaker Recognition Application¶

Markov models are used significantly in speech recognition systems, and used heavily in the domains of natural language processing, machine learning, and AI. These models can define a probabilistic mechanism for randomly generating sequences over some alphabet of symbols. A k-th order Markov model tracks the last k letters as the context for the present letter. We will build a module called Markov that will work for any positive value of k provided. This module, naturally, resides in markovian/models/markov.py.
While we use the term ``letter,” we will actually work with all characters, whether they be letters, digits, spaces, or punctuation, and will distinguish between upper- and lower-case letters.
Building the Markov Model¶
Given a string of text from an unidentified speaker, we will use a Markov model for a known speaker to assess the likelihood that the text was uttered by that speaker. Thus, the first step is building a Markov Model on known text from a speaker. For this assignment, the Markov Model will be represented using your linear probing hash table: LPHashtable. You must use your implementation and not the built-in dictionaries from Python! You will be given an integer value of k at the start of the program. Each key-value pairing inside the table contains string keys with length k and k + 1 and values set to the number of times those keys appeared in the text. For example, let’s say you have a file called speakerA.txt for Speaker A that contains the following text:
This_is_.
We will use this text to create a Markov Model for Speaker A. The algorithm proceeds as follows:
Starting from the beginning of the text for some known speaker:
For each character in the known text, you generate a string of length k that includes the current character plus k - 1 succeeding characters (Note: The model actually works by finding the
kpreceding letters but our way works too because we are using a wrap-around effect). You then will update frequency value by one for the k string inside the hash table.For each character in the known text, you generate a string of length k + 1 that includes the current character plus k succeeding characters. You then will update frequency value by one for the k + 1 string inside the hash table.
For certain characters, they will not have
kork + 1succeeding characters. For example, what are the succeeding characters for the character'.'in thespeakerA.txttext ifk=2? We will wrap around. We will think of the string circularly, and glue the beginning of the string on to the end to provide a source of the needed context. For instance, if k = 2, and we have the string"ABCD", then the letters of context for'D'will be"DAB"(fork+1) and"DA"(fork).
Below is a diagram of all of the k and k + 1 length strings that are generated from the speakerA.txt file given that k = 2:
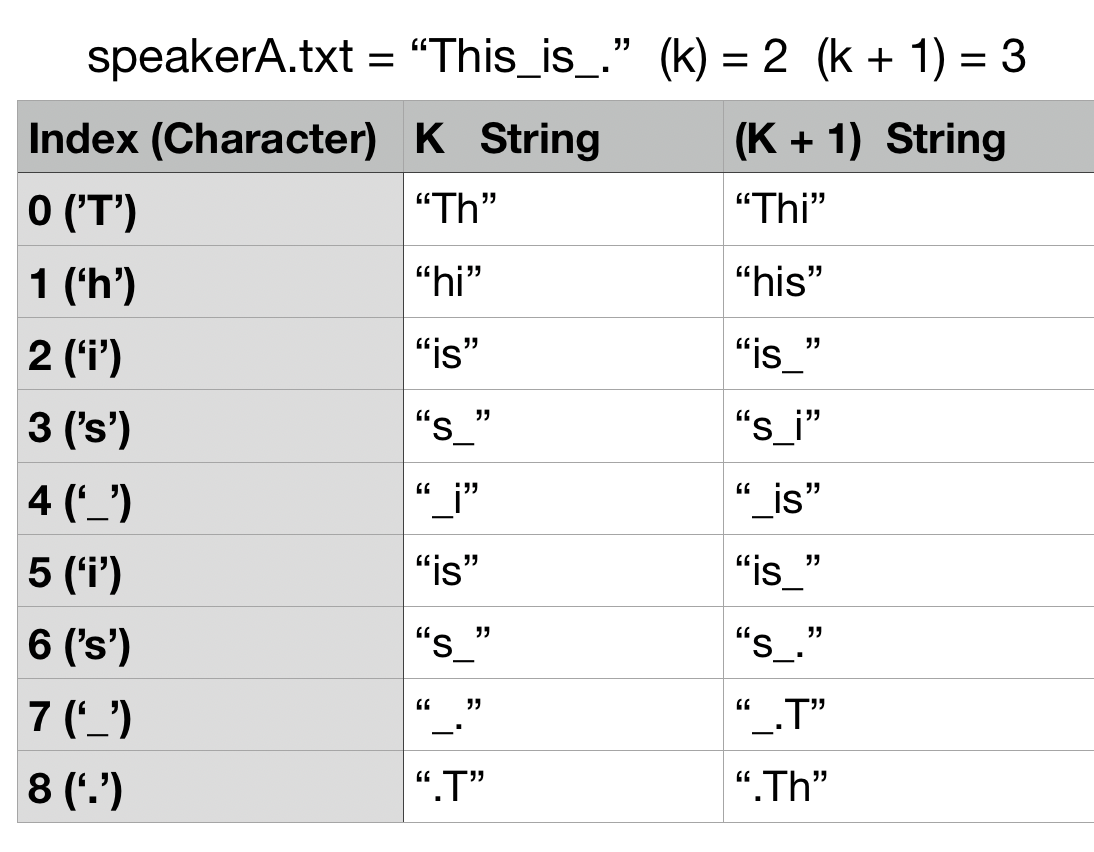
The Markov Model will contain the number of times those k and k + 1 were generated via the known text. Thus, for the speakerA.txt file, the Markov Model generated will be the following:
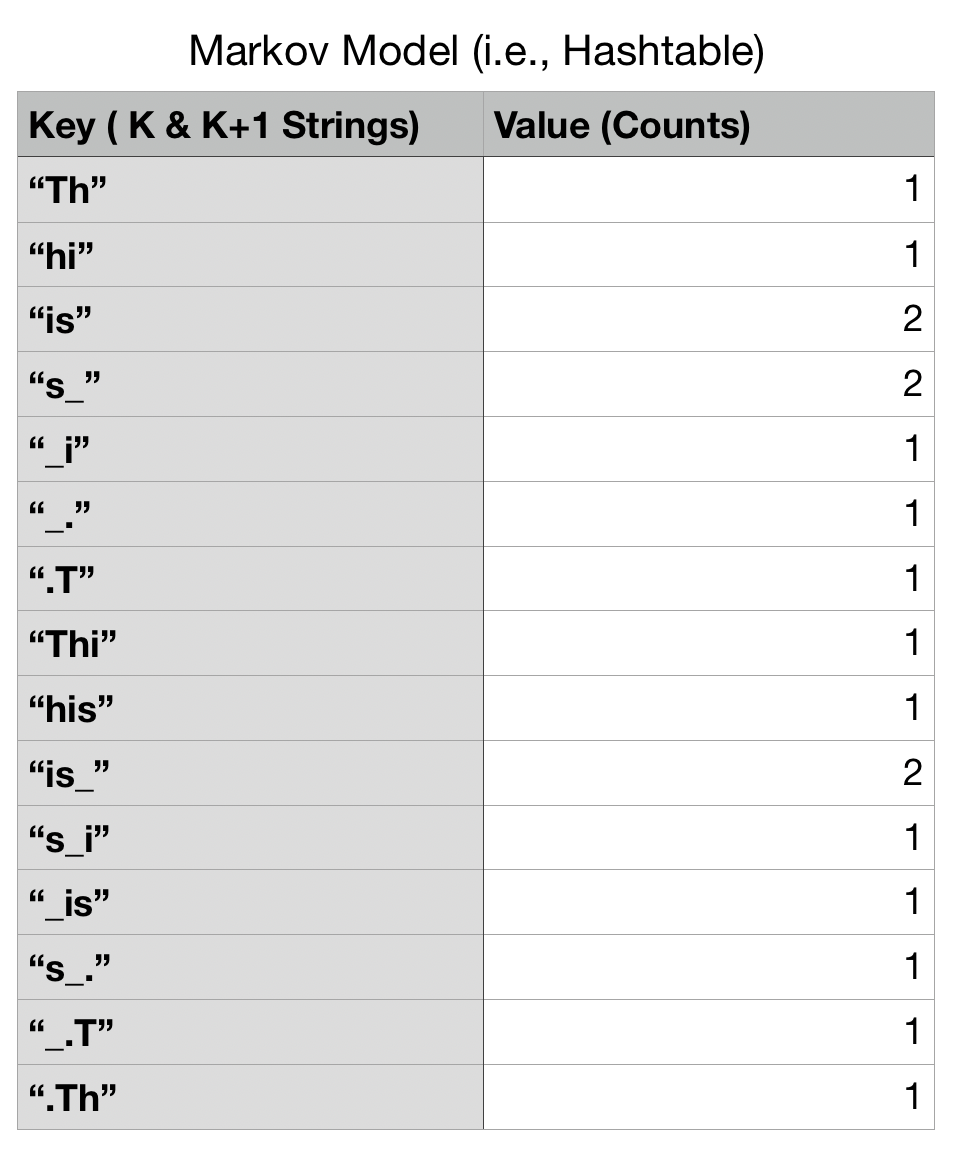
Most of the k and k + 1 strings were only generated once but some such as "is" were generated by processing the character at index 0 and index 5.
Determining the likelihood of unidentified text¶
As we stated earlier, given a string of text from an unidentified speaker, we will use the Markov model for a known speaker to assess the likelihood that the text was uttered by that speaker. Likelihood, in this context, is the probability of the model generating the unknown sequence. If we have built models for different speakers, then we will have likelihood values for each, and will choose the speaker with the highest likelihood as the probable source.
These probabilities can be very small, since they take into account every possible phrase of a certain length that a speaker could have uttered. Therefore, we expect that all likelihoods are low in an absolute sense, but will still find their relative comparisons to be meaningful. Very small numbers are problematic, however, because they tax the precision available for floating-point values. The solution we will adopt for this problem is to use log probabilities instead of the probabilities themselves. This way, even a very small number is represented by a negative value in the range between zero and, for instance, -20. If our log probabilities are negative and we want to determine which probability is more likely, will the greater number (the one closer to zero) represent the higher or lower likelihood, based on how logarithms work?
Note that when we use the Prelude’s math.log function (i.e., we will calculate natural logarithms). Your code should use this base for its logarithms. While any base would suffice to ameliorate our real number precision problem, we will be comparing your results to the results from our implementation, which itself uses natural logs.
The process of determining likelihood given a model is similar to the initial steps of building the Markov Model in the previous section.
Starting from the beginning of the text for some unknown speaker:
For each character in the unknown text, you generate a string of length
kthat includes the current character plusk - 1succeeding characters. You lookup thiskstring in the hash table and store its frequency count in a variable.For each character in the known text, you generate a string of length
k + 1that includes the current character plusksucceeding characters. You lookup thisk + 1string in the hash table and store its frequency count in a variable.For certain characters, they will not have
kork + 1succeeding characters. You will use the same wrap around mechanism as described previously.Now let’s determine the likelihood, we need to keep in mind that we are constructing the model with one set of text and using it to evaluate other text. The specific letter sequences that appear in that new text are not necessarily guaranteed ever to have appeared in the original text. Consequently, we are at risk of dividing by zero. It turns out that there is a theoretically-justifiable solution to this issue, called Laplace smoothing. We modify the simple equation above by adding to the denominator the number of unique characters that appeared in the original text we used for modeling. For instance, if every letter in the alphabet appeared in the text, we add 26. (In practice, the number is likely to be greater, because we distinguish between upper- and lower-case letters, and consider spaces, digits, and punctuation as well.) Because we have added this constant to the denominator, it will never be zero. Next, we must compensate for the fact that we have modified the denominator; a theoretically sound way to balance this is to add one to the numerator. Symbolically, if
Nis the number of times we have observed the $k$ succeeding letters andMis the number of times we have observed those letters followed by the present letter, andSis the size of the “alphabet” of possible characters, then our probability is
For example, lets say you have file called speakerC.txt (i.e., the unidentified text):
This
Calculating the total likelihood will be done in the following way using the model we built from the speakerA.txt text:
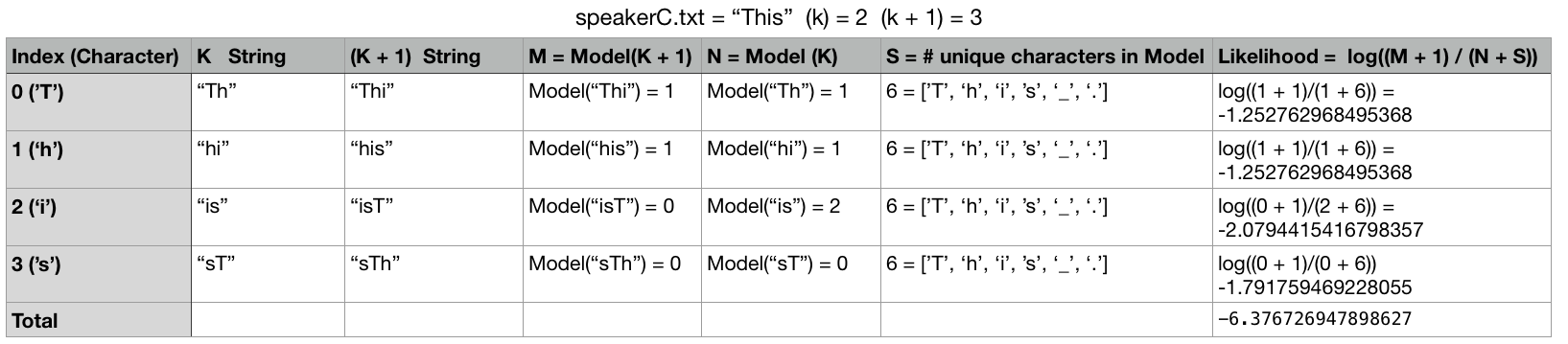
You will perform this calculation for each Markov Model and chose model that produces the highest likelihood total.
A few things to remember
When we say
Model(K)we are looking at the hash table inside the model and retrieving the counts for that string.Sis the number of unique characters that we encountered when building the model. When building the model you need to create a set of all the unique characters.
Task 3: Implementing the Markov Model¶
Inside the markovian/models/markov.py, you will a implement the Markov class with the following instance methods:
A constructor (i.e,
__init__) method that takes in a value ofkand a string of text to create the model. The markov class will use a hash table as its internal state to represent the markov model. You will use yourLPHashtableclass to define an attribute to represent the internal hash tables. You will define one or more hash tables withHASH_CELLSmany cells; we have provided this constant to be a suitable number that is a good starting size for your hash tables, although they will have to grow significantly to accommodate all the statistics you will learn as you scan over the sample text we have provided. You can define the hash table as follows:LPHashtable(HASH_CELLS, 0).identify_speaker(speech1, speech2, speech3, order)- This function is implemented for you already. It is called by theapp.run()method with three strings (i.e.,``(speech1, speech2, speech3`` and a value ofk(i.e.,order). It constructs the models for the speakers that uttered the first two strings, calculates the normalized log probabilities that those two speakers uttered the third string, and return these two probabilities in a tuple (with the first entry being the probability of the first speaker). Finally, it compares the probabilities and place in the third slot of your returned tuple, a conclusion of which speaker was most likely.log_probabilitymethod yields the likelihood that a particular speaker uttered a specified string of text, this probability may be misleading because it depends upon the length of the string. Because there are many more possible strings of a greater length, and these probabilities are calculated across the universe of all possible strings of the same length, we should expect to see significant variance in these values for different phrases. To reduce this effect, we will divide all of our probabilities by the length of the string, to yield normalized ones. To be clear, this division does not occur inlog_probability, but rather inidentify_speaker. Also, note that we will be calculating log probabilities, under different models, for the same string. Thus, string length differences are not a factor during a single run of our program. Rather, we choose to normalize in this fashion because we want outputs for different runs to be more directly comparable when they may pertain to different length quotes being analyzed.
While these are the only methods whose details we are dictating, your code will benefit dramatically from a careful selection of helper functions.
Running the Application¶
We have provided a set of files containing text from United States presidential debates from the 2004 and 2008 general elections. In the 2004 election, George W. Bush debated John Kerry; in the 2008 debates, Barack Obama went up against John McCain. We have provided single files for Bush, Kerry, Obama, and McCain to use to build models. These files contain all the text uttered by the corresponding candidate from two debates. We have also provided directories from the third debates of each election year, containing many files, appropriately labeled, that have remarks made by one of the candidates.
Here’s a sample use of the application:
The following command line will allow you to test with the specified files:
$ ipython -m markovian speakerA.txt speakerB.txt unidentified.txt k
where the first two file names represent the text files that will be used to build the two models, and the third file name is that of the file containing text whose speaker we wish to determine using the Markov approach. The final argument is the order (\(k\)) of the Markov models to use, an integer.
Here’s a sample use:
$ ipython -m markovian markovian/data/bush1+2.txt markovian/data/kerry1+2.txt markovian/data/bush-kerry3/BUSH-0.txt 2 Speaker A: -2.1670591295191572 Speaker B: -2.2363636778055525 Conclusion: Speaker A is most likely
We have also provided the usual style of test code in
test_markov.py.
Debugging suggestions¶
A few debugging suggestions:
Make sure you have chosen the right data structure for the Markov model!
Check your code for handling the wrap-around carefully. It is a common source of errors.
Test the code for constructing a Markov model using a very small string, such as
"abcabd". Check your data structure to make sure that you have the right set of keys and the correct counts.Make sure you are using the correct value for \(S\): the number of unique characters that appeared in the training text.
Obtaining your test score¶
Your “Completeness” portion of the programming assignments, is determined by the automated tests. To get your score for the automated tests, simply run the following from the Linux command-line. (Remember to leave out the $ prompt when you type the command.)
cd markovian/tests
py.test
./grader.py
Grading¶
Programming assignments will be graded according to a general rubric. Specifically, we will assign points for completeness, correctness, design, and style. (For more details on the categories, see our PA Rubric page.)
The exact weights for each category will vary from one assignment to another. For this assignment, the weights will be:
Completeness: 65%
Correctness: 15%
Design: 10%
Style: 10%
The completeness part of your score will be determined using automated tests. To get your score for the automated tests, simply run the grader script, as described above.
Cleaning up¶
Before you submit your final solution, you should, remove
any
printstatements that you added for debugging purposes andall in-line comments of the form: “YOUR CODE HERE” and “REPLACE …”
Also, check your code against the style guide. Did you use good variable names? Do you have any lines that are too long, etc.
Do not remove header comments, that is, the triple-quote strings that describe the purpose, inputs, and return values of each function.
As you clean up, you should periodically save your file and run your code through the tests to make sure that you have not broken it in the process.
Submission¶
You will be submitting your work through Gradescope (linked from our Canvas site). The process will be the same as with the short exercises: Gradescope will fetch your files directly from your PA1 repository on GitHub, so it is important that you remember to commit and push your work! You should also get into the habit of making partial submissions as you make progress on the assignment; remember that you’re allowed to make as many submissions as you want before the deadline.
To submit your work, go to the “Gradescope” section on our Canvas site. Then, click on “Programming Assignment #1”. This is the same process as last quarter to connect your Github repository to Gradescope. You will see a “Connect to GitHub” button. Pressing that button will take you to a GitHub page asking you to confirm that you want to authorize Gradescope to access your GitHub repositories. Just click on the green “Authorize gradescope” button.
Then, under “Repository”, make sure to select your uchicago-CAPP30122-win-2022/pa1-$GITHUB_USERNAME.git repository.
Under “Branch”, just select “main”.
Finally, click on “Upload”. An autograder will run, and will report back a score. Please note that this autograder runs the exact same tests (and the exact same grading script) described in the section above. If there is a discrepancy between the tests when you run them on your computer, and when you submit your code to Gradescope, please let us know.
Acknowledgment¶
This assignment is based on one developed by Rob Schapire with contributions from Kevin Wayne.